
分析 (1)根据去分母、去括号、移项、合并同类项、系数化为1,可得答案;
(2)根据去分母、去括号、移项、合并同类项、系数化为1,可得答案;
解答 解:(1)去分母,得12-2(2x+1)=3(1+x)
去括号,得12-4x-2=3+3x
移项,得-4x-3x=3-12+2
合并同类项,得-7x=-7
系数互为1,得x=1;
(2)原方程可变形为$\frac{3x+5}{2}$=$\frac{2x-1}{3}$,( 分数的性质 )
去分母,得3(3x+5)=2(2x-1).( 等式性质2 )
去括号,得9x+15=4x-2.( 乘法分配律 )
移项,得9x-4x=-15-2.( 等式性质1 )
合并,得5x=-17.( 合并同类项 )
系数化为1,得x=-$\frac{17}{5}$.( 等式性质2 ),
故答案为:分数的性质,去分母,乘法分配律,移项,系数化为1.
点评 本题考查了解一元一次方程,去分母是解题关键,不含分母的项不要漏乘分母的最小公倍数.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 14 | B. | 16 | C. | 8+5$\sqrt{2}$ | D. | 14+$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲、乙两人从同一地点出发到达同一目的地,如图是他们离出发地的路程y(百米)与时间x(分钟)的关系图象,下列结论不正确的是( )
甲、乙两人从同一地点出发到达同一目的地,如图是他们离出发地的路程y(百米)与时间x(分钟)的关系图象,下列结论不正确的是( )| A. | 甲经过54分钟到达目的地 | |
| B. | 乙比甲晚出发12分钟 | |
| C. | 当乙到达目的地时甲、乙两人所走的路程比为5:9 | |
| D. | 若乙到达目的地后继续往前走,当甲到达目的地时乙比甲多走140米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
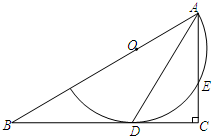 如图,△ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AC于点E,连接AD.
如图,△ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AC于点E,连接AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com