
分析 (1)根据二次根式的意义得出a的值,进而求出c的值,即可求出点A,C坐标,利用两点间的距离公式求出AC;
(2)①先判断出△ABE≌△CAO得出BE=2,AE=6,即可求出点E的坐标,进而求出直线AB的解析式,利用BD⊥AB求出直线BD解析式即可求出点D的坐标;
②先判断出AC∥BD,再利用S△APC=S△ABC,得出点P到直线AC的距离等于AB,即可判断出点P在直线BD上或在直线BD关于直线AC的对称的直线B'P上,即可求出点P的坐标.
解答 解:(1)∵a,c满足c=$\sqrt{a-2}$+$\sqrt{2-a}$+6.
∴a-2≥0,2-a≥0,
∴a=2,
∴c=6,
∴A(0,2),C(6,0),
∴AC=2$\sqrt{10}$;
(2)①如图1,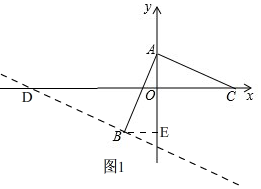 过点B作BE⊥OA于E,
过点B作BE⊥OA于E,
∴∠AEB=90°,
∴∠ABE+∠BAE=90°,
∵AB⊥AC,
∴∠BAE+∠CAO=90°,
∴∠ABE=∠CAO,
在△ABE和△CAO中,$\left\{\begin{array}{l}{∠AEB=∠COA}\\{∠ABE=∠CAO}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△CAO,
∴BE=OA=2,AE=OC=6,
∵OA=2,
∴OE=4,
∴B(-2,-4),
∴直线AB的解析式为y=3x+2,
∵∠ABD=90°,且B(-2,-4),
∴直线BD的解析式为y=-$\frac{1}{3}$x-$\frac{14}{3}$,
当y=0时,x=-14,
∴D(-14,0);
②如图2,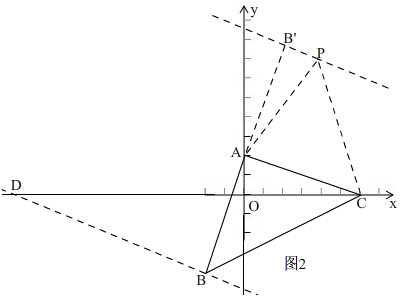 ∵BD⊥AB,AC⊥AB,
∵BD⊥AB,AC⊥AB,
∴BD∥AC,
∴直线AC和BD间的距离是AB,
设点P到AC的距离为h,
∴S△ACP=$\frac{1}{2}$AC•h,
∵S△ABC=$\frac{1}{2}$AC•AB,而S△APC=S△ABC
∴$\frac{1}{2}$AC•h=$\frac{1}{2}$AC•AB,
∴h=AB,
Ⅰ、点P在直线AC下方时,点P在直线BD上,
∵P(m,2m),
由(2)知,直线BD的解析式为y=-$\frac{1}{3}$x-$\frac{14}{3}$,
∴2m=-$\frac{1}{3}$m-$\frac{14}{3}$,
∴m=-2,
∴P(-2,-4)此时和点B重合,不符合题意,舍去;
Ⅱ、当点P在直线AC上方时,
∵BA⊥AC,A(0,2),B(-2,-4),
∴点B关于直线AC的对称点B'的坐标为(2,8),
∴直线B'P的解析式为y=-$\frac{1}{3}$x+$\frac{26}{3}$,
∵点P在直线B'P上,
∴2m=-$\frac{1}{3}$m+$\frac{26}{3}$,
∴m=$\frac{26}{7}$,
∴P($\frac{26}{7}$,$\frac{52}{7}$).
故答案为:($\frac{26}{7}$,$\frac{52}{7}$).
点评 此题是三角形综合题,主要考查了全等三角形的判断和性质,待定系数法求直线解析式,平行线的判断,解(1)关键利用二次根式的意义求出a的值,解(2)的关键是求出点B的坐标,解(3)的关键是利用S△APC=S△ABC,判断出点P在直线BD上或直线B'P上.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
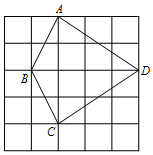 如图,5×5网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,四边形ABCD的顶点A、B、C、D均在格点上,求四边形ABCD的周长.(结果化为最简二次根式).
如图,5×5网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,四边形ABCD的顶点A、B、C、D均在格点上,求四边形ABCD的周长.(结果化为最简二次根式).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{(100x+y)-(100y+x)=144}\\{y=7x+4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{(100x+y)-(10y+x)=144}\\{y=7x+4}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{(10y+x)-(100x+y)=144}\\{y=7x+4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{(100x+y)-(10x+y)=144}\\{y=7x+4}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
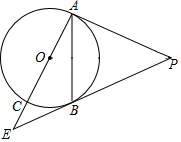 如图,PA,PB是⊙O的切线,切点分别为A,B,AC是⊙O的直径,AC,PB的延长线交于点E,若tan∠BAE=$\frac{1}{2}$,求sin∠E的值.
如图,PA,PB是⊙O的切线,切点分别为A,B,AC是⊙O的直径,AC,PB的延长线交于点E,若tan∠BAE=$\frac{1}{2}$,求sin∠E的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com