
分析 (1)根据有理数的加减混合运算顺序和法则逐步计算可得;
(2)根据有理数的加减混合运算顺序和法则逐步计算可得;
(3)根据有理数的加减混合运算顺序和法则逐步计算可得;
(4)根据有理数的加减混合运算顺序和法则逐步计算可得.
解答 解:(1)原式=23-11+2-16
=23+2-(11+16)
=25-27
=-2;
(2)原式=(-26.54+18.54)+(6.4-6.4)
=-8;
(3)原式=-0.5-7.5+3.25+2.75
=-8+6
=-2;
(4)原式=-20+14+18-12
=-32+32
=0.
点评 本题主要考查有理数的加减混合运算,掌握有理数的加减混合运算顺序和法则是解题的关键.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:解答题
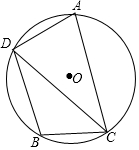 如图,⊙O中,$\widehat{AB}$=$\widehat{AC}$,D为$\widehat{AB}$上任意一点,若cos∠BDC=$\frac{3}{4}$,求tan∠ADC的值.
如图,⊙O中,$\widehat{AB}$=$\widehat{AC}$,D为$\widehat{AB}$上任意一点,若cos∠BDC=$\frac{3}{4}$,求tan∠ADC的值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
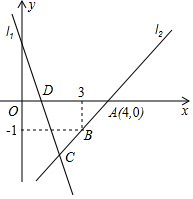 如图,直线l1的解析式为y=-2x+3,且l1与x轴交于点D,直线l2经过点A(4,0)、B(3,-1),直线l1、l2交于点C.
如图,直线l1的解析式为y=-2x+3,且l1与x轴交于点D,直线l2经过点A(4,0)、B(3,-1),直线l1、l2交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
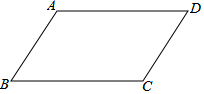 如图,已知四边形ABCD是平行四边形,若点E,F分别在边BC,AD上,连接AE,CF,请再从下列三个备选条件中,选择一个恰当的条件,使四边形AECF是平行四边形,画出符合要求的示意图,并予以证明.
如图,已知四边形ABCD是平行四边形,若点E,F分别在边BC,AD上,连接AE,CF,请再从下列三个备选条件中,选择一个恰当的条件,使四边形AECF是平行四边形,画出符合要求的示意图,并予以证明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 14 | B. | 16 | C. | 8+5$\sqrt{2}$ | D. | 14+$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com