
【题目】如图,在![]() ABCD中,以点A为圆心,AB长为半径作圆弧,交AD于点F,再分别以B、F为圆心,大于线段BF的一半长为半径作圆弧,两弧交于点P,作射线AP交BC边于点E,若AB=10,BF=12,则AE的长为( )
ABCD中,以点A为圆心,AB长为半径作圆弧,交AD于点F,再分别以B、F为圆心,大于线段BF的一半长为半径作圆弧,两弧交于点P,作射线AP交BC边于点E,若AB=10,BF=12,则AE的长为( )
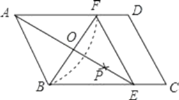
A.12B.44C.16D.18
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
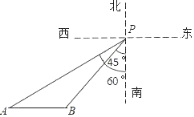
【题目】在某海域,一艘海监船在P处检测到南偏西45°方向的B处有一艘不明船只,正沿正西方向航行,海监船立即沿南偏西60°方向以40海里/小时的速度去截获不明船只,经过1.5小时,刚好在A处截获不明船只,求不明船只的航行速度.(![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留一位小数).
≈1.73,结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
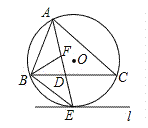
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
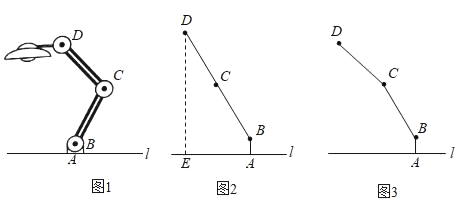
【题目】如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC、CD与AB始终在同一平面上.
(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.
(2)将(1)中的连杆CD再绕点C逆时针旋转,经试验后发现,如图3,当∠BCD=150°时台灯光线最佳.求此时连杆端点D离桌面l的高度比原来降低了多少厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
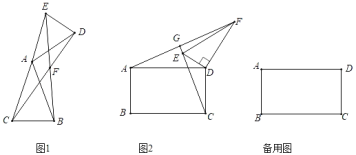
【题目】(1)如图1,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=30°,连接CD,BE交于点F.![]() = ;∠BFD= ;
= ;∠BFD= ;
(2)如图2,在矩形ABCD和△DEF中,AB=![]() AD,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点G.求
AD,∠EDF=90°,∠DEF=60°,连接AF交CE的延长线于点G.求![]() 的值及∠AGC的度数,并说明理由.
的值及∠AGC的度数,并说明理由.
(3)在(2)的条件下,将△DEF绕点D在平面内旋转,AF,CE所在直线交于点P,若DE=1,AD=![]() ,求出当点P与点E重合时AF的长.
,求出当点P与点E重合时AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com