
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
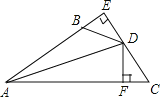
(1)、求证:AD平分∠BAC;
(2)、直接写出AB+AC与AE之间的等量关系.
【答案】(1)、证明过程见解析;(2)、AB+AC=2AE.
【解析】
试题分析:(1)、根据垂直得出△BDE与△CDE均为直角三角形,然后根据BD=CD,BE=CF得出三角形全等,从而得出DE=DF,根据角平分线的逆定理得出答案;(2)、根据角平分线得出∠EAD=∠CAD,结合∠E=∠AFD=90°得出∠ADE=∠ADF,从而说明△AED≌△AFD,根据全等得出AE=AF,最后根据AB+AC=AE﹣BE+AF+CF得出答案.
试题解析:(1)、∵DE⊥AB于E,DF⊥AC于F, ∴∠E=∠DFC=90°,∴△BDE与△CDE均为直角三角形,
∵![]() ,∴△BDE≌△CDF, ∴DE=DF,即AD平分∠BAC;
,∴△BDE≌△CDF, ∴DE=DF,即AD平分∠BAC;
、AB+AC=2AE.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 角平分线上的点到这个角两边的距离相等
B. 角平分线就是角的对称轴
C. 如果两个角相等,那么这两个角互为对顶角
D. 有一条公共边的两个角互为补角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球.每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中约有红球个。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在山顶上有一座电视塔,在塔顶B处,测得地面上一点A的俯角α=60°,在塔底C处测得的俯角β=45°,已知BC=60m,求山高CD(精确到1m,![]() ≈1.732)
≈1.732)
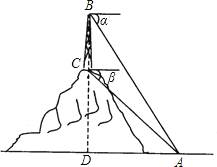
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=- 2x2 - 4x - 5经过平移后得到抛物线y=- 2x2,平移方法是( )
A. 向左平移1个单位,再向下平移3个单位
B. 向左平移1个单位,再向上平移3个单位
C. 向右平移1个单位,再向下平移3个单位
D. 向右平移1个单位,再向上平移3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级某班期末考试语文得“优”的有15人,数学得“优”的有18人,两门功课都得“优”的有8人,两门功课都没有得“优”的有20人,则这个班共有人。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com