
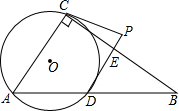
 如图,Rt△ABC中,∠ACB=90°,过A、C两点作⊙O,交边AB于D,PC、PD为⊙O的切线.
如图,Rt△ABC中,∠ACB=90°,过A、C两点作⊙O,交边AB于D,PC、PD为⊙O的切线.分析 (1)连接OC,OD,OP,CD,根据切线的性质得出PC=PD,∠OCP=∠ODP=90°,然后证得△OCP≌△ODP得出∠POC=∠POD=$\frac{1}{2}$∠COD,从而求得∠A=∠POD,进而即可证得结论;
(2)根据切线的性质得出PC=PD,∠OCP=∠ODP=90°OP⊥CD,进而得出∠PDO=∠PFD=90°,根据cos∠P=$\frac{PE}{PC}$=$\frac{1}{3}$得出cos∠P=$\frac{PE}{PD}$=$\frac{1}{3}$,求得PC=PD=3,PE=1,然后根据勾股定理得出CE=$\sqrt{P{C}^{2}-P{E}^{2}}$=2$\sqrt{2}$,CD=$\sqrt{C{E}^{2}+D{E}^{2}}$=2$\sqrt{3}$,PF=$\sqrt{P{D}^{2}-D{F}^{2}}$=$\sqrt{6}$,通过证得△OPD∽△DPF,得出$\frac{OD}{PD}$=$\frac{DF}{PF}$,即$\frac{OD}{3}$=$\frac{\sqrt{3}}{\sqrt{6}}$,
即可求得OD=$\frac{3\sqrt{2}}{2}$.
解答 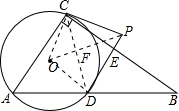 解:(1)连接OC,OD,OP,CD,
解:(1)连接OC,OD,OP,CD,
∵PC、PD为⊙O的切线,
∴PC=PD,∠OCP=∠ODP=90°,
在△OCP和△ODP中
$\left\{\begin{array}{l}{OC=OD}\\{PC=PD}\\{OP=OP}\end{array}\right.$
∴△OCP≌△ODP(SSS),
∴∠POC=∠POD=$\frac{1}{2}$∠COD,$∠OPC=∠OPD=\frac{1}{2}∠CPD$,
∵$∠A=\frac{1}{2}$∠COD,
∴∠A=∠POD,
∵∠ACB=∠ODP=90°,
∴∠OPD=∠B,
∴∠CPD=2∠B;
(2)∵PC、PD为⊙O的切线,
∴OP⊥CD,OD⊥PD,
∴∠PDO=∠PFD=90°,
∵PD⊥BC,
∴cos∠P=$\frac{PE}{PC}$
∵PC=PD,
∴cos∠P=$\frac{PE}{PD}$=$\frac{1}{3}$
∵DE=2,
∴PD=3,
∴PC=3,
∴CE=$\sqrt{P{C}^{2}-P{E}^{2}}$=2$\sqrt{2}$,
∴CD=$\sqrt{C{E}^{2}+D{E}^{2}}$=2$\sqrt{3}$,
∴DF=$\frac{1}{2}$CD=$\sqrt{3}$,
∴PF=$\sqrt{P{D}^{2}-D{F}^{2}}$=$\sqrt{6}$,
∵∠PDO=∠PFD=90°,∠OPD=∠DPF,
∴△OPD∽△DPF,
∴$\frac{OD}{PD}$=$\frac{DF}{PF}$,即$\frac{OD}{3}$=$\frac{\sqrt{3}}{\sqrt{6}}$,
∴OD=$\frac{3\sqrt{2}}{2}$.
点评 本题考查了切线的性质,三角形相似的判断和性质,勾股定理的应用,直角三角函数等,作出辅助线根据直角三角形是解题的关键.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
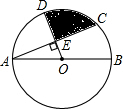 如图,⊙O的直径AB=4cm,AC是⊙O的弦,∠BAC=30°,点D在⊙O上,OD⊥AC于E,则阴影部分的面积为( )
如图,⊙O的直径AB=4cm,AC是⊙O的弦,∠BAC=30°,点D在⊙O上,OD⊥AC于E,则阴影部分的面积为( )| A. | $\frac{20π-15\sqrt{3}}{30}$cm2 | B. | $\frac{24π-15\sqrt{3}}{30}$cm2 | C. | $\frac{20π-18\sqrt{3}}{30}$cm2 | D. | $\frac{20π-15\sqrt{3}}{20}$cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
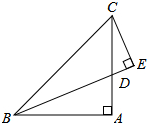 如图,已知,∠BAC=90°,AB=AC,BD是∠ABC的平分线,且CE⊥BD交BD延长线于点E.
如图,已知,∠BAC=90°,AB=AC,BD是∠ABC的平分线,且CE⊥BD交BD延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
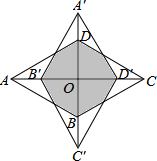 如图,菱形ABCD的一个内角是60°,将它绕对角线的交点O顺时针旋转90°后得到菱形A′B′C′D′.旋转前后两菱形重叠部分多边形的周长为8$\sqrt{3}$-8,则菱形ABCD的边长为2.
如图,菱形ABCD的一个内角是60°,将它绕对角线的交点O顺时针旋转90°后得到菱形A′B′C′D′.旋转前后两菱形重叠部分多边形的周长为8$\sqrt{3}$-8,则菱形ABCD的边长为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com