Question

10．在Rt△ABC中，∠C=90°，若斜边上的高为h，sinA=$\frac{3}{5}$，则AB的长等于（　　）

• A． $\frac{5}{4}$h
• B． $\frac{5}{3}$h
• C． $\frac{25}{12}$h
• D． $\frac{12}{25}$h

Answer 1

分析 在Rt△ABC中，根据正弦的定义得sinA=$\frac{BC}{AB}$=$\frac{3}{5}$，设BC=3k，则AB=5k，根据勾股定理求出AC=4k；在Rt△ACD中，由h与sinA的值，求出AC=$\frac{5}{3}$h，那么4k=$\frac{5}{3}$h，求出k，进而得到AB．

解答 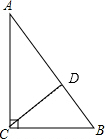解：如图，CD为斜边AB上的高，
在Rt△ABC中，sinA=$\frac{BC}{AB}$=$\frac{3}{5}$，
设BC=3k，则AB=5k，
根据勾股定理，得AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4k；
在Rt△ACD中，sinA=$\frac{CD}{AC}$=$\frac{h}{AC}$=$\frac{3}{5}$，
AC=$\frac{5}{3}$h，
∵4k=$\frac{5}{3}$h，
∴k=$\frac{5}{12}$h，
∴AB=5×$\frac{5}{12}$h=$\frac{25}{12}$h．
故选C．

点评 此题考查了解直角三角形，涉及的知识有：锐角三角函数定义，勾股定理，熟练掌握定理及法则是解本题的关键．