
【题目】如图2是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°,折线NG﹣GH﹣HE﹣EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH. 
(1)如图2①,若点H在线段OB时,则 ![]() 的值是;
的值是;
(2)如果一级楼梯的高度HE=(8 ![]() +2)cm,点H到线段OB的距离d满足条件d≤3cm,那么小轮子半径r的取值范围是 .
+2)cm,点H到线段OB的距离d满足条件d≤3cm,那么小轮子半径r的取值范围是 .
【答案】
(1)![]()
(2)(11﹣3 ![]() )cm≤r≤8cm
)cm≤r≤8cm
【解析】解:(1.)如图2①,P为⊙B的切点,连接BP并延长,作OL⊥BP于点L,交GH于点M, 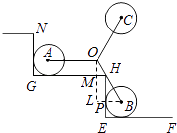
∴∠BPH=∠BLO=90°,
∵AO∥GH,
∴BL∥AO∥GH,
∵∠AOB=120°,
∴∠OBL=60°,
在RT△BPH中,HP= ![]() BP=
BP= ![]() r,
r,
∴ML=HP= ![]() r,
r,
OM=r,
∵BL∥GH,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
故答案为: ![]() .
.
(2.)作HD⊥OB,P为切点,连接BP,PH的延长线交BD延长线于点L,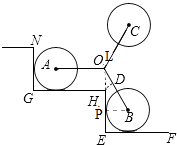
∴∠LDH=∠LPB=90°,
∴△LDH∽△LPB,
∴ ![]() =
= ![]() ,
,
∵AO∥PB,∠AOD=120°,
∴∠B=60°,
∴∠BLP=30°,
∴DL= ![]() DH,LH=2DH,
DH,LH=2DH,
∵HE=(8 ![]() +2)cm
+2)cm
∴HP=8 ![]() +2﹣r,
+2﹣r,
PL=HP+LH=8 ![]() +2﹣r+2DH,
+2﹣r+2DH,
∴ ![]() =
= ![]() ,解得DH=
,解得DH= ![]() r﹣4
r﹣4 ![]() ﹣1,
﹣1,
∵0cm≤DH≤3cm,
∴0≤ ![]() r﹣4
r﹣4 ![]() ﹣1≤3,
﹣1≤3,
解得:(11﹣3 ![]() )cm≤r≤8cm.
)cm≤r≤8cm.
故答案为:(11﹣3 ![]() )cm≤r≤8cm.
)cm≤r≤8cm.
(1)作P为⊙B的切点,连接BP并延长,作OL⊥BP于点L,交GH于点M,求出ML,OM,根据 ![]() =
= ![]() 求解,(2)作HD⊥OB,P为切点,连接BP,PH的延长线交BD延长线于点L,由△LDH∽△LPB,得出
求解,(2)作HD⊥OB,P为切点,连接BP,PH的延长线交BD延长线于点L,由△LDH∽△LPB,得出 ![]() =
= ![]() ,再根据30°的直角三角形得出线段的关系,得到DH和r的关系式,根据0≤d≤3的限制条件,列不等式组求范围.
,再根据30°的直角三角形得出线段的关系,得到DH和r的关系式,根据0≤d≤3的限制条件,列不等式组求范围.


科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内时,∠A与∠1+∠2之间有始终不变的关系是( )

A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2 C. 3∠A=∠1+∠2 D. 3∠A=2(∠1+∠2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(3)班为了组队参加学校举行的“五水共治”知识竞赛,在班里选取了若干名学生,分成人数相同的甲、乙两组,进行了四次“五水共治”模拟竞赛,成绩优秀的人数和优秀率分别绘制成如图统计图. 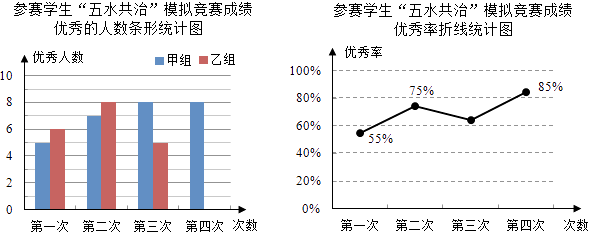
根据统计图,解答下列问题:
(1)第三次成绩的优秀率是多少?并将条形统计图补充完整;
(2)已求得甲组成绩优秀人数的平均数 ![]() =7,方差
=7,方差 ![]() =1.5,请通过计算说明,哪一组成绩优秀的人数较稳定?
=1.5,请通过计算说明,哪一组成绩优秀的人数较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在棋盘中建立如图的直角坐标系,三颗棋子A,O,B的位置如图,它们分别是(﹣1,1),(0,0)和(1,0). 
(1)如图2,添加棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴;
(2)在其他格点位置添加一颗棋子P,使A,O,B,P四颗棋子成为一个轴对称图形,请直接写出棋子P的位置的坐标.(写出2个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心, ![]() cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班有50位学生,每位学生都有一个序号,将50张编有学生序号(从1号到50号)的卡片(除序号不同外其它均相同)打乱顺序重新排列,从中任意抽取1张卡片.
(1)在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率;
(2)若规定:取到的卡片上序号是k(k是满足1≤k≤50的整数),则序号是k的倍数或能整除k(不重复计数)的学生能参加某项活动,这一规定是否公平?请说明理由;
(3)请你设计一个规定,能公平地选出10位学生参加某项活动,并说明你的规定是符合要求的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①, ![]() 是
是![]() 的边
的边![]() 上的高,且
上的高,且![]() cm,
cm,![]() cm,点
cm,点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动,其速度与时间的关系如图②所示,设点
运动,其速度与时间的关系如图②所示,设点![]() 的运动时间为
的运动时间为![]() (s),
(s),![]() 的面积为
的面积为![]() (cm2 ).
(cm2 ).
(1)在点![]() 沿
沿![]() 向点
向点![]() 运动的过程中,它的速度是 cm/s,用含
运动的过程中,它的速度是 cm/s,用含![]() 的代数式表示线段
的代数式表示线段![]() 的长是 cm,变量
的长是 cm,变量![]() 与
与![]() 之间的函数表达式为;
之间的函数表达式为;
(2)当![]() 时,求
时,求![]() 的值.当
的值.当![]() 每增加1时,求
每增加1时,求![]() 的变化情况.
的变化情况.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com