
【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心, ![]() cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒) 
【答案】t=2或3≤t≤7或t=8
【解析】解:∵△ABC是等边三角形, ∴AB=AC=BC=AM+MB=4cm,∠A=∠C=∠B=60°,
∵QN∥AC,AM=BM.
∴N为BC中点,
∴MN= ![]() AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,
AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,
分为三种情况:
①如图1,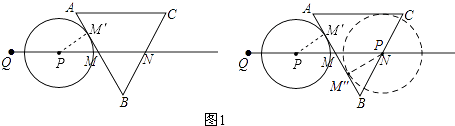
当⊙P切AB于M′时,连接PM′,
则PM′= ![]() cm,∠PM′M=90°,
cm,∠PM′M=90°,
∵∠PMM′=∠BMN=60°,
∴M′M=1cm,PM=2MM′=2cm,
∴QP=4cm﹣2cm=2cm,
即t=2;
②如图2,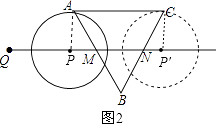
当⊙P于AC切于A点时,连接PA,
则∠CAP=∠APM=90°,∠PMA=∠BMN=60°,AP= ![]() cm,
cm,
∴PM=1cm,
∴QP=4cm﹣1cm=3cm,
即t=3,
当⊙P于AC切于C点时,连接P′C,
则∠CP′N=∠ACP′=90°,∠P′NC=∠BNM=60°,CP′= ![]() cm,
cm,
∴P′N=1cm,
∴QP=4cm+2cm+1cm=7cm,
即当3≤t≤7时,⊙P和AC边相切;
③如图3,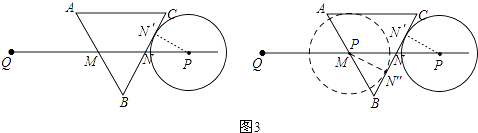
当⊙P切BC于N′时,连接PN′
则PN′= ![]() cm,∠PN′N=90°,
cm,∠PN′N=90°,
∵∠PNN′=∠BNM=60°,
∴N′N=1cm,PN=2NN′=2cm,
∴QP=4cm+2cm+2cm=8cm,
即t=8;
注意:由于对称性可知,当P点运动到AB右侧时也存在⊙P切AB,此时PM也是为2,即P点为N点,同理可得P点在M点时,⊙P切BC.这两点都在第二种情况运动时间内.
故答案为:t=2或3≤t≤7或t=8.
求出AB=AC=BC=4cm,MN= ![]() AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,分为三种情况:画出图形,结合图形求出即可;
AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,分为三种情况:画出图形,结合图形求出即可;


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线相交于点A1,得∠A1;∠A1BC和∠A1CD的平分线相交于点A2,得∠A2;…;∠A2018BC和∠A2018CD的平分线交于点A2019,则∠A2019=________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.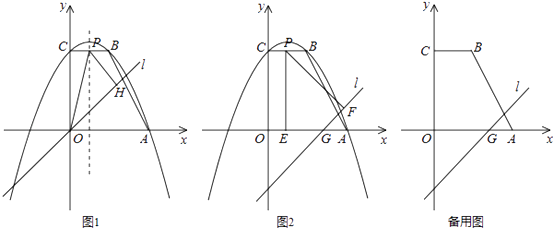
(1)求该抛物线的函数解析式;
(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积;
②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小龙沿着一条笔直的马路进行长跑比赛,小明在比赛过程中始终领先小龙,并匀速跑完了全程,小龙匀速跑了几分钟后提速和小明保持速度一致,又过了1分钟,小龙因体力问题,不得已又减速,并一直以这一速度完成了余下的比赛, 完成比赛所用时间比小明多了1分钟,已知小明跑后4分20秒时领先小龙175米,小明与小龙之间的距离![]() (米)与他们所用时间
(米)与他们所用时间![]() (分钟)之间的函数关系如图所示.有下列说法:①小明到达终点时,小龙距离终点还有225米;②小明的速度是300米/分;③小龙提速前的速度是200米/分;④比赛全程为1 500米.其中正确的是( )
(分钟)之间的函数关系如图所示.有下列说法:①小明到达终点时,小龙距离终点还有225米;②小明的速度是300米/分;③小龙提速前的速度是200米/分;④比赛全程为1 500米.其中正确的是( )

A. ①②③ B. ②③④
C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图2是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°,折线NG﹣GH﹣HE﹣EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH. 
(1)如图2①,若点H在线段OB时,则 ![]() 的值是;
的值是;
(2)如果一级楼梯的高度HE=(8 ![]() +2)cm,点H到线段OB的距离d满足条件d≤3cm,那么小轮子半径r的取值范围是 .
+2)cm,点H到线段OB的距离d满足条件d≤3cm,那么小轮子半径r的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数y2= ![]() x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
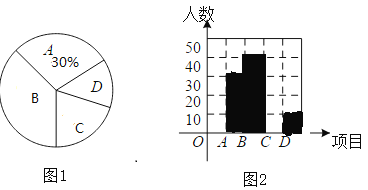
【题目】学校开展“阳光体育”活动,学生会为了解学生最喜欢哪一种球类运动项目,![]() :足球、
:足球、![]() :乒乓球、
:乒乓球、![]() :篮球、
:篮球、![]() :羽毛球,随机抽取了一部分学生进行调查(要求每位同学只能选择一种喜欢的球类),并将调查结果绘制成如下两个不完整的统计图,如图1,图2,请你根据图中提供的信息解答下列问题。
:羽毛球,随机抽取了一部分学生进行调查(要求每位同学只能选择一种喜欢的球类),并将调查结果绘制成如下两个不完整的统计图,如图1,图2,请你根据图中提供的信息解答下列问题。
(1)在这次调查中,一共调查了_____名学生;
(2)在图1扇形统计图中,求出“![]() ”部分所对应的圆心角等于_____度;
”部分所对应的圆心角等于_____度;
(3)求喜欢篮球的同学占被抽查人数的百分比,并补全频数分布折线统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在AB直线一侧C、D两点,在AB上找一点P,使C、D、P三点组成的三角形的周长最短,找出此点并说明理由.
(2)如图2,在∠AOB内部有一点P,是否在OA、OB上分别存在点E、F,使得E、F、P三点组成的三角形的周长最短,找出E、F两点,并说明理由.
(3)如图3,在∠AOB内部有两点M、N,是否在OA、OB上分别存在点E、F,使得E、F、M、N,四点组成的四边形的周长最短,找出E、F两点,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com