
����Ŀ����1����ͼ1����ABֱ��һ��C��D���㣬��AB����һ��P��ʹC��D��P������ɵ������ε��ܳ���̣��ҳ��˵㲢˵�����ɣ�
��2����ͼ2������AOB�ڲ���һ��P���Ƿ���OA��OB�Ϸֱ���ڵ�E��F��ʹ��E��F��P������ɵ������ε��ܳ���̣��ҳ�E��F���㣬��˵�����ɣ�
��3����ͼ3������AOB�ڲ�������M��N���Ƿ���OA��OB�Ϸֱ���ڵ�E��F��ʹ��E��F��M��N���ĵ���ɵ��ı��ε��ܳ���̣��ҳ�E��F���㣬��˵�����ɣ�

���𰸡���1���𰸼���������2���𰸼���������3���𰸼�������
��������
��1�����ڡ�PCD���ܳ���PC+CD+PD����CD�Ƕ�ֵ����ֻ����ֱ��l����һ��P��ʹPC+PD��С�������C����l�ĶԳƵ�ΪC�䣬ʹPC+PD��С����ʹPC��+PD��С��
��2����P����OA��OB�ĶԳƵ�C��D������CD��OA��OB��E��F����ʱ��PEF�ܳ�����Сֵ��
��3����ͼ3����M����OA�ĶԳƵ�C������OB�ĶԳƵ�D������CD����OA��E��OB��F����ʱʹ��E��F��M��N���ĵ���ɵ��ı��ε��ܳ������
��1����ͼ1����C����ֱ��AB�ĶԳƵ�C�䣬����C��D��AB�ڵ�P�����P������Ҫ�����ĵ㣮����������
��l��ȡ��ͬ��P�ĵ�P�䣬����CP�䡢DP�䣮
��C��C�����ֱ��l�Գ�����PC��PC�䣬P��C��P��C�䣬��C��P+DP��C��P��+DP�䣬��PC+DP��CP��+DP�䣬��CD+CP+DP��CD+CP��+DP�䣮����CDP�ܳ�С�ڡ�CDP���ܳ���
��2����ͼ2����P����OA�ĶԳƵ�C������OB�ĶԳƵ�D������CD����OA��E��OB��F�����E��F������Ҫ�����ĵ�������������
��OA��OB��ȡ��ͬ��E��F�ĵ�E�䣬F�䣮����CE�䡢E��P��PF�䡢DF�䣮
��C��P����ֱ��OA�Գ�����PE��CE��CE�䣽PE�䣬PF��DF��PF�䣽DF�䣬��PE+EF+PF��CE+EF+DF��PE��+PF��+E��F�䣽CE��+E��F��+DF�䣮
��CE+EF+DF��CE��+E��F��+DF�䣬��PE+EF+PF��PE��+E��F��+PF�䣻
��3����ͼ3����M����OA�ĶԳƵ�C����N����OB�ĶԳƵ�D������CD����OA��E��OB��F�����E��F������Ҫ�����ĵ㣮����������
��OA��OB��ȡ��ͬ��E��F�ĵ�E�䣬F�䣬����CE�䡢E��F�䣬DF�䣮
��C��M����ֱ��OA�Գ�����ME��CE��CE�䣽ME�䣬NF��DF��NF�䣽DF�䣬�ɣ�2����֪MN+ME+EF+NF��MN+ME��+E��F��+F��D��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������QN��ȱߡ�ABC������AB��BC�ֱ��ڵ�M��N����AC��QN��AM=MB=2cm��QM=4cm������P�ӵ�Q������������QN��ÿ��1cm���ٶ������ƶ�������t�룬�Ե�PΪԲ�ģ� ![]() cmΪ�뾶��Բ���ABC�ı����У��е��ڱ��ϣ�����д��t��ȡ��һ��ֵ����λ���룩
cmΪ�뾶��Բ���ABC�ı����У��е��ڱ��ϣ�����д��t��ȡ��һ��ֵ����λ���룩 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��
��1������ABC����ԭ��O�����ĶԳƵġ�A1B1C1 ��
��2����д����B����y��ԳƵĵ�B2������ �� ������B2����ƽ��h��λ��ʹ�����ڡ�A1B1C1�ڲ����������߽磩��ֱ��д��h��ֵ��д�������һ�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����AP����ABC�����ƽ���ߣ�����PB��PC��
��1����ͼ1����BPƽ����ABC������ACB=30�㣬д����APB�Ķ�����
��2����ͼ1����P��A���غϣ���֤��AB+AC��PB+PC��
��3����ͼ2��������P��PM��BA����BA�ӳ�����M�㣬����BPC=��BAC����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC������Բ���е�ֱ�ΪD��E��F����A=80�㣬��PΪ��O������һ�㣨����E��F�غϣ������EPF= �� 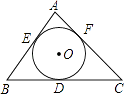
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڷ���Ϊ25 km/h�������£�һ�ܷɻ�˳���A�����ɵ�B����Ҫ��5.6h����������ͬ���ĺ���Ҫ��6h����
(1)��ʱ��ܷɻ�����һ���ߵ�ƽ�����٣�
(2)������֮��ĺ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и���
��1�����㣺 ![]() +2��1��6cos30�㣮
+2��1��6cos30�㣮
��2���Ȼ�������ֵ����a��1��2��a��a+2��������a=�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ���������ĸ����ۣ���b��0����c��0����b2��4ac��0����a��b+c��0��������ȷ�ĸ����У� �� 
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����֪��ABC �У����� A��0����2����B��2����4����C��4����1����
��1���������ABC ���� y ��ԳƵ�ͼ�Ρ�A1B1C1��
��2��д����A1B1C1 ���������ꣻ
��3�����ABC �������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com