
| A. | 140元 | B. | 150元 | C. | 160元 | D. | 180元 |
分析 设每张床位提高x个单位,每天收入为y元,根据等量关系“每天收入=每张床的费用×每天出租的床位”可求出y与x之间的函数关系式,运用公式求最值即可.
解答 解:设每张床位提高x个20元,每天收入为y元.
则有y=(100+20x)(100-10x)
=-200x2+1000x+10000.
当x=-$\frac{b}{2a}$=$\frac{1000}{200×2}$=2.5时,可使y有最大值.
又x为整数,则x=2时,y=11200;
x=3时,y=11200;
则为使租出的床位少且租金高,每张床收费=100+3×20=160元,
故选:C.
点评 本题考查二次函数的实际应用,建立二次函数的模型解决实际问题是解题的关键.


科目:初中数学 来源: 题型:填空题
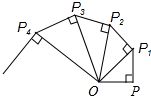 如图,OP=1,过P作PP1⊥OP,且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1,且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2,且P2P3=1,得OP3=2;…依此法继续作下去,得OP2016=$\sqrt{2017}$.
如图,OP=1,过P作PP1⊥OP,且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1,且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2,且P2P3=1,得OP3=2;…依此法继续作下去,得OP2016=$\sqrt{2017}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
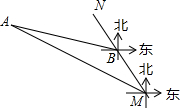 如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据:$\sqrt{3}$≈1.732)
如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据:$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
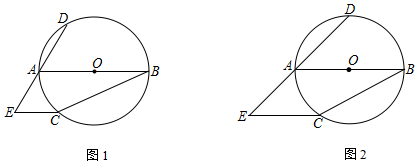
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-6,-4) | B. | (-6,-3) | C. | (-6,-2) | D. | (-6,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
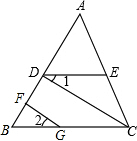 已知:如图,CD⊥AB,GF⊥AB,∠B=∠ADE.
已知:如图,CD⊥AB,GF⊥AB,∠B=∠ADE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com