
【题目】如图,在矩形ABCD中AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么![]() 的值是_________.
的值是_________.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
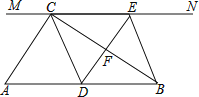
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,
①四边形![]() 是平行四边形;
是平行四边形;
②![]() 是等腰三角形;
是等腰三角形;
③四边形![]() 的周长是
的周长是![]() ;
;
④四边形![]() 的面积是16.
的面积是16.
则以上结论正确的是![]()
![]()

A. ①②③B. ①②④C. ①③④D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=![]() 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
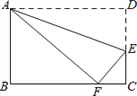
【题目】如图,在Rt△ABC中,![]() ,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明理由;
(3)若D为AB中点,则当![]() =______时,四边形BECD是正方形.
=______时,四边形BECD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点![]() .
.![]() .
.![]() ,完成系列问题:
,完成系列问题:
![]()
(1)将点![]() 向右移动六个单位长度到点
向右移动六个单位长度到点![]() ,在数轴上表示出点
,在数轴上表示出点![]() .
.
(2)在数轴上找到点![]() ,使点
,使点![]() 到
到![]() .
.![]() 两点的距离相等.并在数轴上标出点
两点的距离相等.并在数轴上标出点![]() 表示的数.
表示的数.
(3)在数轴上有一点![]() ,满足点
,满足点![]() 到点
到点![]() 与点
与点![]() 到点
到点![]() 的距离和是
的距离和是![]() ,则点
,则点![]() 表示的数是__________.
表示的数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
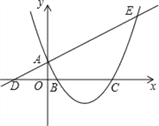
【题目】如图,已知直线y=![]() x+1与y轴交于点A,与x轴交于点D,抛物线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y= ![]() x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标__________.
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为带分数,如![]() 我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”,如
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”,当分子的次数小于分母的次数时,我们称之为“真分式”,如![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如:![]() 这样的分式就是真分式。类似的,假分式也可以化为带分式(即:整式与真分式的和的形式),如:
这样的分式就是真分式。类似的,假分式也可以化为带分式(即:整式与真分式的和的形式),如:
![]()
请解决下列问题:
(1)分式![]() 是_____分式(填“真”或“假”);
是_____分式(填“真”或“假”);
(2)将假分式![]() 化为带分式;
化为带分式;
(3)若分式![]() 的值为整数,直接写出所有符合条件的正整数
的值为整数,直接写出所有符合条件的正整数![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
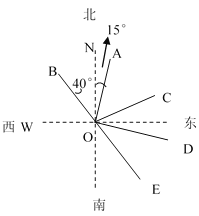
【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OE是射线OB的反向延长线.
(1)求射线OC的方向角;
(2)求∠COE的度数;
(3)若射线OD平分∠COE,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com