
【题目】已知一次函数y=x+6和反比例函数y=![]() (k≠0).
(k≠0).
(1)k满足什么条件时,这两个函数在同一坐标系中的图象有两个公共点?
(2)设(1)中的公共点为A和B,则∠AOB是锐角还是钝角?
【答案】(1) k>-9(k≠0) ;(2)见解析.
【解析】
(1)当比例系数符号相同或组成方程组整理后的一元二次方程的判别式大于0时,两个函数在同一坐标系xOy中的图象有两个公共点;
(2)结合(1)中k的取值范围,分情况探讨∠AOB是锐角还是钝角.
(1)分两种情况:
①当比例系数符号相同,即k<0时,这两个函数在同一坐标系xOy中的图象有两个公共点;
②解方程组 ,
,
整理得:x2-6x+k=0,
∵它们有两个公共点,
∴36-4k>0,
解得k<9,在第一,三象限,
∴0<k<9.
故当0<k<9或k<0时,这两个函数在同一坐标系xOy中的图象有两个公共点;
(2)①当k<0时,如图1,点A、点B分别在第二、四象限,连接OA、OB,可知∠AOB>∠xoy=90°,故∠AOB为钝角;

②当0<k<9时,如图2,点A、点B都在第一象限,连接OA、OB,可知∠AOB<∠xOy=90°,故∠AOB为锐角.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】食品加工是一种专业技术,就是把原料经过人为处理形成一种新形式的可直接食用的产品,这个过程就是食品加工.比如用小麦经过碾磨、筛选、加料搅拌、成型烘干,成为饼干,就是属于食品加工的过程.下表给出了甲、乙、丙三种原料中的维生素A、B的含量(单位:g/kg).
原料甲 | 原料乙 | 原料丙 | |
维生素A的含量 | 4 | 6 | 4 |
维生素B的含量 | 8 | 2 | 4 |
将甲、乙、丙三种原料共100kg混合制成一种新食品,其中原料甲xkg,原料乙ykg.
(1)这种新食品中,原料丙的含量__________kg,维生素B的含量__________g;(用含![]() 、
、![]() 的式子表示)
的式子表示)
(2)若这种新食品中,维生素A的含量至少为440g,维生素B的含量至少为480g,请你证明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角板中的两个直角顶点重合在一起,即按如图所示的方式叠放在一起,其中∠A=60°,∠B=30,∠D=45°.
(1)若∠BCD=45°,求∠ACE的度数.
(2)若∠ACE=150°,求∠BCD的度数.
(3)由(1)、(2)猜想∠ACE与∠BCD存在什么样的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1
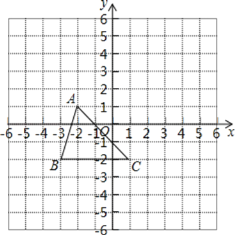
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若直线BC上有一点P,使△PAC的面积是△ABC面积的2倍,直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点O为坐标原点,点A(3a,2a)在第一象限,过点A向x轴作垂线,垂足为点B,连接OA,S△AOB=12,点M从O出发,沿y轴的正半轴以每秒2个单位长度的速度运动,点N从点B出发以每秒3个单位长度的速度向x轴负方向运动,点M与点N同时出发,设点M的运动时间为t秒,连接AM,AN,MN.
(1)求a的值;
(2)当0<t<2时,
①请探究∠ANM,∠OMN,∠BAN之间的数量关系,并说明理由;
②试判断四边形AMON的面积是否变化?若不变化,请求出其值;若变化,请说明理由。
(3)当OM=ON时,请求出t的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一段6000米的道路由甲、乙两个工程队负责完成,已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.
(1)求甲、乙两工程队每天各完成多少米?
(2)如果甲工程队每天需工程费700元,乙工程队每天需工程费500元,甲工程队单独施工4天后由甲乙两个工程队共同完成余下的工程,则完成此项工程共需要多少费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
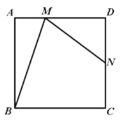
【题目】如图,在边长为 a 的正方形 ABCD 中, M 是边 AD 上一动点(点 M 与点 A 、 D 不重合), N 是 CD 的中点,且CBMNMB ,则 tan ABM (___________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ACB中,∠ACB=90°,AC=BC,D为AB上一点,连结CD,将CD绕C点逆时针旋转90°至CE,连结DE,过C作CF⊥DE交AB于F,连结BE.
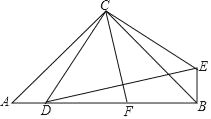
(1)求证:AD=BE;
(2)求证:AD2+BF2=DF2;
(3)若∠ACD=15°,CD=![]() +1,求BF.
+1,求BF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com