
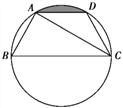
【题目】如图,已知点A,B,C,D均在已知圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,四边形ABCD的周长为10.
(1)求此圆的半径;
(2)求图中阴影部分的面积.
【答案】(1)圆的半径为2;(2)![]() -
-![]()
【解析】试题分析:(1)已知AC平分∠BCD,由角平分线的定义可得∠ACD=∠ACB,
再由AD∥BC,即可得∠ACB=∠DAC=∠ACD,因∠ADC=120°,根据等腰三角形的性质和圆内接四边形互补可得∠ACB=∠DAC=∠ACD =30°,∠B=60°,根据圆周角定理的推论可得AB=AD=DC,且∠BAC=90°,即可BC为直径;设圆心为O,AB=x,则BC=2AB=2x,
由四边形ABCD的周长为10cm,可得x+x+x+2x=10,解得x=2,即可求得⊙O的半径为2;(2)设圆心为O,连接OA、OD,由(1)可知OA=OD=AD,可得△AOD为等边三角形,根据等边三角形的性质可得∠AOD=60°;因AD∥BC,可得![]() ,即可得
,即可得![]() .
.
试题解析:
(1)∵AC平分∠BCD,
∴∠ACD=∠ACB,
又∵AD∥BC,
∴∠ACB=∠DAC=∠ACD,
而∠ADC=120°,
∴∠ACB=∠DAC=∠ACD =30°,∠B=60°,
∴AB=AD=DC,且∠BAC=90°,
∴BC为直径,设圆心为O,AB=x,则BC=2AB=2x,
又∵四边形ABCD的周长为10cm,
∴x+x+x+2x=10,解得x=2,
即⊙O的半径为2.
(2)设圆心为O,连接OA、OD,
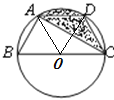
由(1)可知OA=OD=AD,
∴△AOD为等边三角形,
∴∠AOD=60°;
∵AD∥BC,
∴![]() ,
,
∴![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图所示,
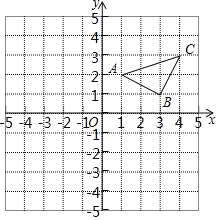
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小,写出作法.
查看答案和解析>>
科目:初中数学 来源: 题型:
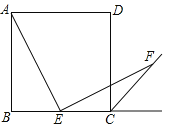
【题目】八年级下册教材第69页习题14:四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.求证:AE=EF.这道题对大多数同学来说,印象深刻数学课代表在做完这题后,她把这题稍作改动,如图,四边形ABCD是正方形,点E是边BC的三等分点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,那么AE=EF还成立吗?如果成立,给予证明,如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从王同学和李同学中挑选一人参加县知识竞赛在五次选拔测试中他俩的成绩如下表.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
王同学 | 60 | 75 | 100 | 90 | 75 |
李同学 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
王同学 | 80 | 75 | 75 | _____ |
李同学 |
|
|
|
|
(2)在这五次测试中,成绩比较稳定的同学是谁若将80分以上(含80分)的成绩视为优秀,则王同学、李同学在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
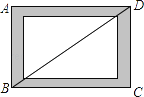
A. 四边形ABCD由矩形变为平行四边形 B. BD的长度增大
C. 四边形ABCD的面积不变 D. 四边形ABCD的周长不变
查看答案和解析>>
科目:初中数学 来源: 题型:
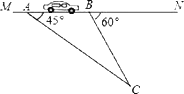
【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对点(x,y)的一次操作变换记为p1(x,y),定义其变换法则如下:p1(x,y)=(x+y,x-y);且规定Pn(x,y)=P1(Pn-1(x,y))(n为大于1的整数).例如:p1(1,2)=(3,-1),p2(1,2)=p1(p1(1,2))=p1(3,-1)=(2,4),p3(1,2)=p1(p2(1,2))=p1(2,4)=(6,-2).则p2014(1,-1)=( )
A.(0,21006) B.(21007,-21007) C.(0,-21006) D.(21006,-21006)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测“华为P30”手机能畅销,就用1600元购进一批该型号手机壳,面市后果然供不应求,又购进6000元的同种型号手机壳,第二批所购买手机壳的数量是第一批的3倍,但进货单价比第一批贵了2元。
(1)第一批手机壳的进货单价是多少元?
(2)若两次购进于机壳按同一价格销售,全部传完后,为使得获利不少于2000元,那么销售单价至少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:O是直线AB上的一点,![]() 是直角,OE平分
是直角,OE平分![]() .
.
(1)如图1.若![]() .求
.求![]() 的度数;
的度数;
(2)在图1中,![]() ,直接写出
,直接写出![]() 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);
(3)将图1中的![]() 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究![]() 和
和![]() 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com