【题目】已知：如图所示，
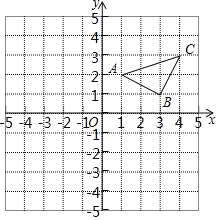
(1)作出△ABC关于y轴对称的△A′B′C′，并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P，使PA+PC最小，写出作法.
【答案】(1)作图见解析，A′(1，2)，B′(3，1)，C′(4，3)；(2)作图见解析.
【解析】试题分析：（1）根据网格结构找出点A、B、C关于y轴对称的点A′、B′、C′的位置，然后顺次连接即可，再根据平面直角坐标系写出各点的坐标；
（2）根据网格结构找出点C关于x轴的对称点C″的位置，连接AC″与x轴相交于点P，根据轴对称确定最短路线问题，点P即为所求作的点．
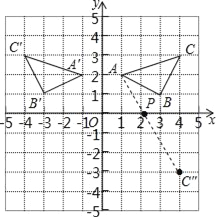
试题解析：（1）△A′B′C′如图所示，A′（﹣1，2），B′（﹣3，1），C′（﹣4，3）；
（2）如图所示，点P即为使PA+PC最小的点．
作法：①作出C点关于x轴对称的点C″（4，﹣3），
②连接C″A交x轴于点P，
点P点即为所求点．
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB=6，BC=4，过对角线BD中点O的直线分别交AB，CD边于点E，F．
（1）求证：四边形BEDF是平行四边形；
（2）当四边形BEDF是菱形时，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
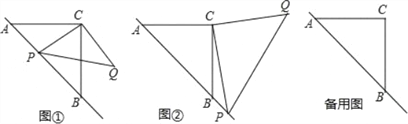
【题目】已知：△ABC是等腰三角形，动点P在斜边AB所在的直线上，以PC为直角边作等腰三角形PCQ，其中∠PCQ=90°，探究并解决下列问题：
（1）如图①，若点P在线段AB上，且AC=1+
，PA=
，则：
①线段PB= ，PC= ；
②猜想：PA2，PB2，PQ2三者之间的数量关系为 ；
（2）如图②，若点P在AB的延长线上，在（1）中所猜想的结论仍然成立，请你利用图②给出证明过程；
（3）若动点P满足
，求
的值．（提示：请利用备用图进行探求）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知高铁的速度比动车的速度快50 km/h，小路同学从苏州去北京游玩，本打算乘坐动车，需要6h才能到达；由于得知开通了高铁，决定乘坐高铁，她发现乘坐高铁比乘坐动车节约72 min．求高铁的速度和苏州与北京之间的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如下两个尚不完整的统计表.调查结果统计表
组别 | 分组（单位：元） | 人数 |
|
| 4 |
|
| 16 |
|
|
|
|
|
|
|
| 2 |
调查结果扇形统计图
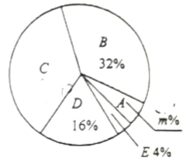
请根据以上图表，解答下列问题：
（1）这次被调查的同学共有 人，
；
（2）求扇形统计图中扇形
的圆心角的度数；
（3）若该校共有学生1000人，请估计每月零花钱的数额
在
范围的人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB＝16，O为AB中点，点C在线段OB上（不与点O，B重合），将OC绕点O逆时针旋转270°后得到扇形COD，AP，BQ分别切优弧
于点P，Q，且点P， Q在AB异侧，连接OP．
（1）求证：AP＝BQ；
（2）当BQ＝4
时，求扇形COQ的面积及
的长（结果保留π）；
（3）若△APO的外心在扇形COD的内部，请直接写出OC的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
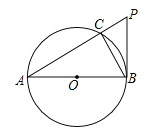
【题目】如图，AB是⊙O的直径，PB与⊙O相切于点B，连接PA交⊙O于点C，连接BC．
（1）求证：∠BAC=∠CBP；
（2）求证：PB2=PCPA；
（3）当AC=6，CP=3时，求sin∠PAB的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
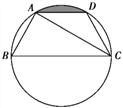
【题目】如图，已知点A，B，C，D均在已知圆上，AD∥BC，CA平分∠BCD，∠ADC=120°，四边形ABCD的周长为10.
(1)求此圆的半径；
(2)求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
