
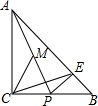
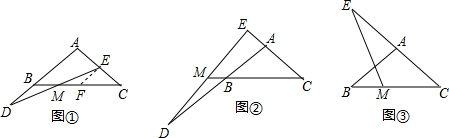
 如图,△ACB为等腰直角三角形,△PBE也为等腰直角三角形,M为AP的中点.
如图,△ACB为等腰直角三角形,△PBE也为等腰直角三角形,M为AP的中点.分析 (1)将△BCE绕点C逆时针旋转90°得到△CAF,连接EF与直线PA交于点M′,连接PF,只要证明△ECF是等腰直角三角形,EM=MF即可.
(2)证明方法类似(1).
解答 (1)证明:将△BCE绕点C逆时针旋转90°得到△CAF,连接EF与直线PA交于点M′,连接PF,
∵CA=CB,∠ACB=90°,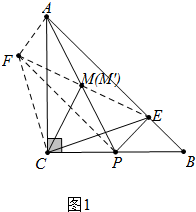
∴∠CAB=∠CBA=∠CAF=45°,
∵EP=EB,∠PEB=90°,∠FAB=∠CAF+∠CAB=90°,
∴∠FAB=∠PEB,
∴FA∥PE,
∵FA=BE-PE,
∴四边形AFPE是平行四边形,
∴AM′=M′P,FM′=M′E,
∴点M与点M′重合,
∵CE=CF,∠ECF=90°,FM=EM,
∴CM=MF=ME,∠MCE=∠MEC=45°,
∴EC=$\sqrt{2}$CM.
(2)结论仍然成立.
证明:如图,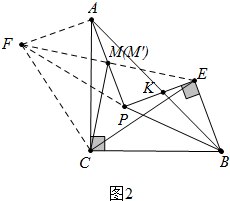 将△BCE绕点C逆时针旋转90°得到△CAF,连接EF与直线PA交于点M′,连接PF,AB与PE交于点K.
将△BCE绕点C逆时针旋转90°得到△CAF,连接EF与直线PA交于点M′,连接PF,AB与PE交于点K.
∵CA=CB,∠ACB=90°,
∴∠CAB=∠CBA=∠CAF=45°,
∵EP=EB,∠PEB=90°,∠FAB=∠CAF+∠CAB=45°+∠CAB,
∠PKB=∠PEB+∠EBK=90°+∠EBK=45°+(45°+∠EBK)=45°+∠CBE,
又∵∠CAF=∠CBE,
∴∠PKB=∠FAB,
∴FA∥PE,
∵FA=BE-PE,
∴四边形AFPE是平行四边形,
∴AM′=M′P,FM′=M′E,
∴点M与点M′重合,
∵CE=CF,∠ECF=90°,FM=EM,
∴CM=MF=ME,∠MCE=∠MEC=45°,
∴EC=$\sqrt{2}$CM.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质,解题的关键是利用旋转添加辅助线,构造平行四边形以及全等三角形,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10.1×108 | B. | 1.01×108 | C. | 1.01×109 | D. | 0.101×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x-1)=56×2 | B. | 2x(x+1)=56 | C. | x(x+1)=56 | D. | x(x-1)=56 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com