
分析 (1)根据二次根式有意义的条件即可得出关于a的一元二次不等式组,解不等式组即可得出a的值,再由分母不为0即可确定a的值,将其代入b中求出b值,进而即可得出$\sqrt{a+b}$的值;
(2)将$\sqrt{a+b}$的值代入方程中即可得出关于k的一元二次方程,解方程即可求出k值,设方程另一个根为x1,根据根与系数的关系即可得出关于x1的一元一次方程,解方程即可得出方程的另一个根.
解答 解:(1)依题意得:$\left\{\begin{array}{l}{a^2}-4≥0\\ 4-{a^2}≥0\end{array}\right.$,
解得:a=±2,
又∵a+2≠0,
∴a≠-2,
∴a=2,b=$\frac{1}{2+2}$=$\frac{1}{4}$,
∴$\sqrt{a+b}=\sqrt{2+\frac{1}{4}}=\frac{3}{2}$.
(2)把$\sqrt{a+b}=\frac{3}{2}$代入方程x2-2x+k2+k=0中,得:$\frac{9}{4}-3+{k^2}+k=0$,
解得:k1=$\frac{1}{2}$,k2=-$\frac{3}{2}$.
设方程另一个根为x1,则:${x_1}+\frac{3}{2}=2$,
解得:x1=$\frac{1}{2}$.
答:k的值为$\frac{1}{2}$或-$\frac{3}{2}$,方程的另一个根为$\frac{1}{2}$.
点评 本题考查了根与系数的关系以及二次根式有意义的条件,根据二次根式有意义的条件求出a的值是解题的关键.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
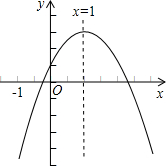 已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论,①abc<0; ②2a+b=0;③b2-4ac<0;④a+b+c>0;⑤a-b+c<0.其中正确的结论有①②④⑤(填序号)
已知二次函数y=ax2+bx+c的图象如图所示,有下列5个结论,①abc<0; ②2a+b=0;③b2-4ac<0;④a+b+c>0;⑤a-b+c<0.其中正确的结论有①②④⑤(填序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com