
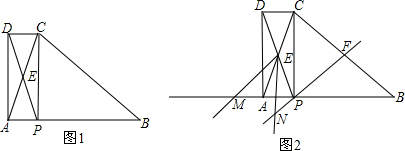
分析 (1)根据AB=BC可证∠CAB=∠ACB,则在△ABC与△AEP中,有两个角对应相等,根据三角形内角和定理,即可证得;
(2)首先证得?APCD是矩形,则可证得:∠EAM=∠EPN,又由旋转的性质,可得∠MEA=∠NEP,继而可以证明△EAM≌△EPN,从而得到EM=EN.
解答 (1)证明:在△ABC和△AEP中,
∵∠ABC=∠AEP,∠BAC=∠EAP,
∴∠ACB=∠APE,
在△ABC中,AB=BC,
∴∠ACB=∠BAC,
∴∠EPA=∠EAP.
(2)解:EM=EN.
理由:∵EA=EP,
∴∠EPA=$\frac{180°-∠AEP}{2}$=$\frac{180°-∠ABC}{2}$=90°-$\frac{1}{2}$α,
∴∠EAM=180°-∠EPA=180°-(90°-$\frac{1}{2}$α)=90°+$\frac{1}{2}$α,
∵四边形APCD是平行四边形,
∴AC=2EA,PD=2EP,
∵由(1)知∠EPA=∠EAP,
∴EA=EP,
则AC=PD,
∴?APCD是矩形.
∴∠CPB=90°,F是BC的中点,
∴FP=FB,
∴∠FPB=∠ABC=α,
∴∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°-$\frac{1}{2}$α+α=90°+$\frac{1}{2}$α,
∴∠EAM=∠EPN,
∵∠AEP绕点E顺时针旋转适当的角度,得到∠MEN,
∴∠AEP=∠MEN,
∴∠AEP-∠AEN=∠MEN-∠AEN,即∠MEA=∠NEP,
在△EAM和△EPN中,
$\left\{\begin{array}{l}{∠EAM=∠EPN}\\{EA=EP}\\{∠MEA=∠NEP}\end{array}\right.$,
∴△EAM≌△EPN(ASA),
∴EM=EN.
点评 本题主要考查了等腰三角形的性质,以及矩形的判定方法,在旋转中找到题目中存在的相等的线段以及相等的角是解决本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
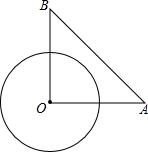 如图,在Rt△AOB中,OB=OA=6,动点C在以点O为圆心,3为半径的⊙O上,OC,OD是两条互相垂直的半径,且点C、D按顺时针方向排列,连接AD,BC,当直线BC为⊙O的切线时,猜想OC与AD的位置关系,并证明.
如图,在Rt△AOB中,OB=OA=6,动点C在以点O为圆心,3为半径的⊙O上,OC,OD是两条互相垂直的半径,且点C、D按顺时针方向排列,连接AD,BC,当直线BC为⊙O的切线时,猜想OC与AD的位置关系,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
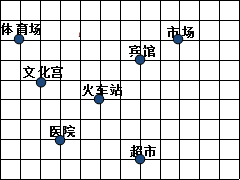 如图,这是某市部分简图,请按要求画出平面直角坐标系,分别写出各地的坐标.
如图,这是某市部分简图,请按要求画出平面直角坐标系,分别写出各地的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$=$\frac{a^2}{b^2}$ | B. | $\frac{a}{b}$=$\frac{ab}{ab}$ | C. | $\frac{a}{b}$=$\frac{a+2c}{b+2c}$(c≠0) | D. | $\frac{a}{b}$=$\frac{ac}{bc}$(c≠0) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
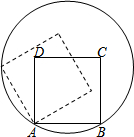 如图,已知正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点逆时针旋转,使点D落在⊙O上.若正方形ABCD的边长和⊙O的半径均为6cm,则点D运动的路径长为πcm.
如图,已知正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点逆时针旋转,使点D落在⊙O上.若正方形ABCD的边长和⊙O的半径均为6cm,则点D运动的路径长为πcm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 3 | C. | -1或3 | D. | -1或-$\frac{5}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -4 | B. | -6 | C. | 4 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com