
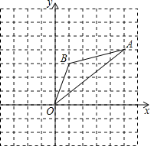
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1.
(1)画出△A1OB1.
(2)在旋转过程中点B所经过的路径长为_______.
(3)求在旋转过程中线段AB扫过的图形的面积.
【答案】(1)见解析;(2)l=![]() ;(3)s=
;(3)s=![]() .
.
【解析】
(1)将OA、OB分别绕点O逆时针旋转90°,可得线段OA1 、OB1,然后连接A1B1,△A1OB1即为所求;
(2)根据勾股定理求出OB,然后利用弧长公式计算即可;
(3)根据勾股定理求出OA,然后由旋转可知:S△A1OB1= S△AOB,然后根据扇形面积公式分别算出S扇形A1OA和S扇形B1OB,由图可知线段AB扫过的图形的面积=S扇形A1OA+S△A1OB1-S扇形B1OB-S△AOB代入计算即可.
解:(1)将OA、OB分别绕点O逆时针旋转90°,可得线段OA1 、OB1,然后连接A1B1,如图所示:△A1OB1即为所求;
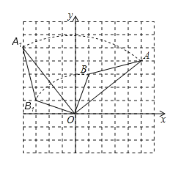
(2)由勾股定理可得:![]()
∴旋转过程中点B所经过的路径长l=![]() ;
;
(3)由勾股定理可知:![]()
由旋转可知:S△A1OB1= S△AOB
由扇形的面积公式:S扇形A1OA=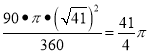 ,S扇形B1OB=
,S扇形B1OB=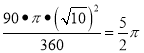
由图可知:线段AB扫过的图形的面积=S扇形A1OA+S△A1OB1-S扇形B1OB-S△AOB=![]()


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
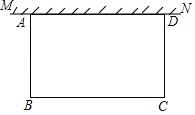
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,点A(3,3),点B(4,0),点C(0,-1).
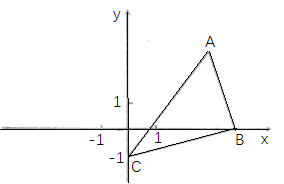
(1)以点C为中心,把△ABC逆时针旋转90°,画出旋转后的图形△A’B’C’(要求尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,
①点A经过的路径AA’的长为________;(结果保留![]() )
)
②写出B’的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
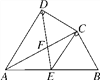
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,连接CE,连接DE交AC于F,AD=4,AB=6.
(1)求证:△ADC∽△ACB;
(2)求AC的值;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
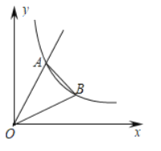
【题目】如图,正比例函数y1=k1x的图象与反比例函数y2=![]() (x>0)的图象相交于点A(
(x>0)的图象相交于点A(![]() ,2
,2![]() ),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是_____.
),点B是反比例函数图象上一点,它的横坐标是3,连接OB,AB,则△AOB的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
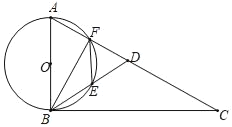
【题目】如图,D为直角△ABC中斜边AC上一点,且AB=AD,以AB为直径的⊙O交AD于点F,交BD于点E,连接BF,BF.
(1)求证:BE=FE;
(2)求证:∠AFE=∠BDC;
(3)已知:sin∠BAE=![]() ,AB=6,求BC的长.
,AB=6,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为![]() 的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形。
的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形。
(1)要使这两个正方形的面积之和等于![]() ,那么这段铁丝剪成两段后的长度分别是多少?
,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于![]() 吗?若能,求出两段铁丝的长度;若不能,请说明理由。
吗?若能,求出两段铁丝的长度;若不能,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com