
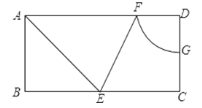
【题目】如图,矩形ABCD中,BC=2AB=4,AE平分∠BAD交边BC于点E,∠AEC的分线交AD于点F,以点D为圆心,DF为半径画圆弧交边CD于点G,则![]() 的长为________
的长为________
【答案】(2﹣![]() )π.
)π.
【解析】
先由矩形的性质得出,∠BAD=∠B=∠D=90°,AD=BC=4,AD∥BC,根据AE平分∠BAD得到∠BAE=∠EAD=45°,那么△ABE是等腰直角三角形,于是AB=BE=2,AE=![]() AB=2
AB=2![]() . 再由∠AEC的分线交AD于点F,∠AEF=∠CEF,由AD∥BC,得出∠CEF=∠AFE,等量代换得到∠AEF=∠AFE,那么AF=AE=2
. 再由∠AEC的分线交AD于点F,∠AEF=∠CEF,由AD∥BC,得出∠CEF=∠AFE,等量代换得到∠AEF=∠AFE,那么AF=AE=2![]() ,DF=AD﹣AF=4﹣2
,DF=AD﹣AF=4﹣2![]() ,然后根据弧长的计算公式即可求出
,然后根据弧长的计算公式即可求出![]() 的长.
的长.
∵四边形ABCD是矩形,
∴∠BAD=∠B=∠D=90°,AD=BC=4,AD∥BC,
∵AE平分∠BAD交边BC于点E,
∴∠BAE=∠EAD=45°,
∴△ABE是等腰直角三角形,
∴AB=BE=2,AE=![]() AB=2
AB=2![]() ,
,
∵∠AEC的分线交AD于点F,
∴∠AEF=∠CEF,
∵AD∥BC,
∴∠CEF=∠AFE,
∴∠AEF=∠AFE,
∴AF=AE=2![]() ,
,
∴DF=AD﹣AF=4﹣2![]() ,
,
∴![]() 的长为:
的长为:![]() =(2﹣
=(2﹣![]() )π,
)π,
故答案为:(2﹣![]() )π.
)π.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
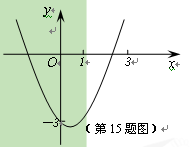
【题目】(11·湖州)如图,已知抛物线![]() 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个
b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是 ▲![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
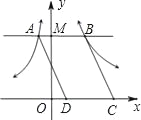
【题目】如图,过y轴上一个动点M作x轴的平行线,交双曲线y=![]() 于点A,交双曲线
于点A,交双曲线![]() 于点B,点C、点D在x轴上运动,且始终保持DC=AB,则平行四边形ABCD的面积是( )
于点B,点C、点D在x轴上运动,且始终保持DC=AB,则平行四边形ABCD的面积是( )
A. 7 B. 10 C. 14 D. 28
查看答案和解析>>
科目:初中数学 来源: 题型:
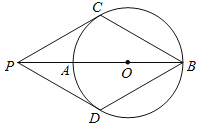
【题目】如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交与点D.
(1)判断CD与⊙O的位置关系并说明理由;
(2)若∠ACB=120°,OA=2,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC和等边△AEF都是半径为R的圆的内接三角形.
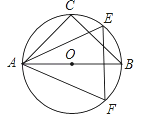
(1)求AF的长.
(2)通过对△ABC和△AEF的观察,请你先猜想谁的面积大,再证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=2,∠BAC=45°.将△ABC绕点A逆时针旋转α度(0<α<180)得到△ADE,B,C两点的对应点分别为点D,E,BD,CE所在直线交于点F.
(1)当△ABC旋转到图1位置时,∠CAD= (用α的代数式表示),∠BFC的度数为 °;
(2)当α=45时,在图2中画出△ADE,并求此时点A到直线BE的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:我渔政310船在南海海面上沿正东方向匀速航行,在A点观测到我渔船C在北偏东60°方向的我国某传统渔场捕鱼作业.若渔政310船航向不变,航行半小时后到达B点,观测到我渔船C在东北方向上.问:渔政310船再按原航向航行多长时间,离渔船C的距离最近?(渔船C捕鱼时移动距离忽略不计,结果不取近似值)
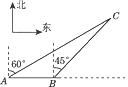
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com