
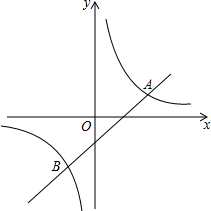
 如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象相交于A(2,1),B两点.
如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象相交于A(2,1),B两点.分析 (1)先将点A(2,1)代入y=$\frac{k}{x}$求得k的值,再将点A(2,1)代入反比例函数的解析式求得n,最后将A、B两点的坐标代入y=x+m,求得m即可.
(2)当反比例函数的值大于一次例函数的值时,即一次函数的图象在反比例函数的图象下方时,x的取值范围.
解答 解:(1)将A(2,1)代入y=$\frac{k}{x}$中,得k=2×1=2,
∴反比例函数的表达式为y=$\frac{2}{x}$,
将A(2,1)代入y=x+m中,得2+m=1,
∴m=-1,
∴一次函数的表达式为y=x-1;
(2)B(-1,-2);
当x<-1或0<x<2时,反比例函数的值大于一次函数的值.
点评 本题考查了反比例函数与一次函数的交点问题,是一道综合题目,解题过程中注意数形结合的应用,是中档题,难度不大.


科目:初中数学 来源: 题型:选择题
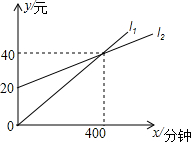 一家电信公司提供两种手机的月通话收费方式供用户选择,其中一种有月租费,另一种无月租费.这两种收费方式的通话费用y(元)与通话时间x(分钟)之间的函数关系如图所示.小红根据图象得出下列结论:
一家电信公司提供两种手机的月通话收费方式供用户选择,其中一种有月租费,另一种无月租费.这两种收费方式的通话费用y(元)与通话时间x(分钟)之间的函数关系如图所示.小红根据图象得出下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
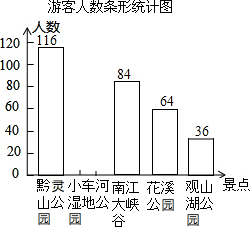 近年来,随着创建“生态文明城市”活动的开展,我市的社会知名度越来越高,吸引了很多外地游客,某旅行社对5月份本社接待外地游客来我市各景点旅游的人数作了一次抽样调查,并将调查结果绘制成如下两幅不完整的统计图表:
近年来,随着创建“生态文明城市”活动的开展,我市的社会知名度越来越高,吸引了很多外地游客,某旅行社对5月份本社接待外地游客来我市各景点旅游的人数作了一次抽样调查,并将调查结果绘制成如下两幅不完整的统计图表:| 景点 | 频数(人数) | 频率 |
| 黔灵山公园 | 116 | 0.29 |
| 小车河湿地公园 | 0.25 | |
| 南江大峡谷 | 84 | 0.21 |
| 花溪公园 | 64 | 0.16 |
| 观山湖公园 | 36 | 0.09 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,⊙P的圆心P为(-3,a),⊙P与y轴相切于点C.直线y=-x被⊙P截得的线段AB长为4$\sqrt{2}$,则过点P的双曲线的解析式为y=-$\frac{3\sqrt{2}+9}{x}$.
如图,在平面直角坐标系xOy中,⊙P的圆心P为(-3,a),⊙P与y轴相切于点C.直线y=-x被⊙P截得的线段AB长为4$\sqrt{2}$,则过点P的双曲线的解析式为y=-$\frac{3\sqrt{2}+9}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com