
 如图,在平面直角坐标系xOy中,⊙P的圆心P为(-3,a),⊙P与y轴相切于点C.直线y=-x被⊙P截得的线段AB长为4$\sqrt{2}$,则过点P的双曲线的解析式为y=-$\frac{3\sqrt{2}+9}{x}$.
如图,在平面直角坐标系xOy中,⊙P的圆心P为(-3,a),⊙P与y轴相切于点C.直线y=-x被⊙P截得的线段AB长为4$\sqrt{2}$,则过点P的双曲线的解析式为y=-$\frac{3\sqrt{2}+9}{x}$. 分析 作PH⊥x轴于H,交直线y=-x于E,作PD⊥AB于D,连结PC、PA,如图,根据切线的性质得PC⊥y轴,则PC=PA=OH=3,再根据垂径定理,由PD⊥AB得AD=BD=$\frac{1}{2}$AB=2$\sqrt{2}$,则可根据勾股定理计算出PD=1,接着利用直线y=-x为第二、四象限的角平分线可判断△HOB和△PDE都为等腰直角三角形,所以EH=OH=3,PE=$\sqrt{2}$PD=$\sqrt{2}$,则P(-3,$\sqrt{2}$+3),然后利用待定系数法求过点P的双曲线的解析式.
解答 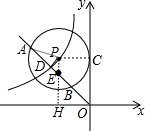 解:作PH⊥x轴于H,交直线y=-x于E,作PD⊥AB于D,连结PC、PA,如图,
解:作PH⊥x轴于H,交直线y=-x于E,作PD⊥AB于D,连结PC、PA,如图,
∵⊙P与y轴相切于点C,
∴PC⊥y轴,
而P(-3,a),
∴PC=3,即⊙P的半径为3,
∴PA=OH=3,
∵PD⊥AB,
∴AD=BD=$\frac{1}{2}$AB=$\frac{1}{2}$×4$\sqrt{2}$=2$\sqrt{2}$,
在Rt△PAD中,PD=$\sqrt{P{A}^{2}-A{D}^{2}}$=$\sqrt{{3}^{2}-(2\sqrt{2})^{2}}$=1,
∵直线y=-x为第二、四象限的角平分线,
∴∠HOB=45°,
易得△HOB和△PDE都为等腰直角三角形,
∴EH=OH=3,PE=$\sqrt{2}$PD=$\sqrt{2}$,
∴PH=PE+EH=$\sqrt{2}$+3,
∴P(-3,$\sqrt{2}$+3),
设过点P的双曲线的解析式为y=$\frac{k}{x}$,
把P(-3,$\sqrt{2}$+3)代入得k=-3($\sqrt{2}$+3)=-3$\sqrt{2}$-9,
∴过点P的双曲线的解析式为y=-$\frac{3\sqrt{2}+9}{x}$.
故答案为y=-$\frac{3\sqrt{2}+9}{x}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了垂径定理、等腰直角三角形的性质和待定系数法求反比例函数解析式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
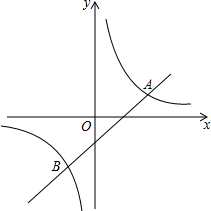 如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象相交于A(2,1),B两点.
如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象相交于A(2,1),B两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
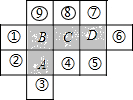 如图,标有数字①~⑨的正方形与标有字母A,B,C,D的正方形大小均相同.现从标有数字的9个正方形中等可能的任选一个,则所选正方形与标有字母的正方形所组成的图形恰可以是一个无盖的正方体的表面展开图,且没有盖的一面恰好与标有字母“A”的一面相对的概率为 ( )
如图,标有数字①~⑨的正方形与标有字母A,B,C,D的正方形大小均相同.现从标有数字的9个正方形中等可能的任选一个,则所选正方形与标有字母的正方形所组成的图形恰可以是一个无盖的正方体的表面展开图,且没有盖的一面恰好与标有字母“A”的一面相对的概率为 ( )| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 沼气池 | 修建费用(万元/个) | 可供使用户数(户/个) | 占地面积(m2/个) |
| A型 | 3 | 20 | 48 |
| B型 | 2 | 3 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 日期 | 一 | 二 | 三 | 四 | 五 | 平均气温 | 方差 |
| 最低气温 | 1 | 3 | 2 | 5 | 4 | 3 |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com