
分析 (1)设甲商品的进价为x元,乙商品的进价为y元,就有x=$\frac{1}{2}$y,3x+y=200,由这两个方程构成方程组求出其解即可以;
(2)设购进甲种商品m件,则购进乙种商品(100-m)件,设利润为W元,根据利润=售价-进价建立解析式,运用一次函数性质就可以求出结论.
解答 解:(1)设甲商品的进价为x元,乙商品的进价为y元,由题意,得:
$\left\{\begin{array}{l}{x=\frac{1}{2}y}\\{3x+y=200}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=40}\\{y=80}\end{array}\right.$.
答:甲商品的进价为40元,乙商品的进价为80元;
(2)设购进甲种商品m件,则购进乙种商品(100-m)件,设利润为W元,由题意,
W=(80-40)m+(130-80)(100-m),
=-10m+5000
∵k=-10<0,
∴W随m的增大而减小,
∵甲种商品不低于40件,
∴m=40时,W最大=4600.
点评 本题考查了列二元一次方程组解实际问题的运用,一次函数的性质的运用;求出利润的解析式运用一次函数的性质求最值是本题的难点.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
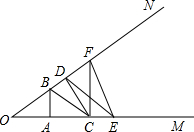 如图,∠MON两边上分别有A,C,E及D,F,B六个点,且S△OAB=S△ABC=S△BCD=S△CDE=S△DEF=1,则S△CDF=$\frac{3}{4}$.
如图,∠MON两边上分别有A,C,E及D,F,B六个点,且S△OAB=S△ABC=S△BCD=S△CDE=S△DEF=1,则S△CDF=$\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,⊙P的圆心P为(-3,a),⊙P与y轴相切于点C.直线y=-x被⊙P截得的线段AB长为4$\sqrt{2}$,则过点P的双曲线的解析式为y=-$\frac{3\sqrt{2}+9}{x}$.
如图,在平面直角坐标系xOy中,⊙P的圆心P为(-3,a),⊙P与y轴相切于点C.直线y=-x被⊙P截得的线段AB长为4$\sqrt{2}$,则过点P的双曲线的解析式为y=-$\frac{3\sqrt{2}+9}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $2\sqrt{6}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{6}}}{6}$ | D. | $\frac{{\sqrt{6}}}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
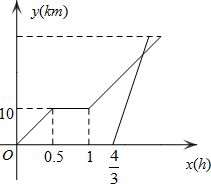 周末,小华骑自行车从家出发到植物园游玩,从家出发0.5小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华离家1小时20分后,爸爸开车沿相同路线前往植物园.如图是他们离家的路程y(km)y与小华离家的时间x(h)的函数图象,已知爸爸开车的速度是小华骑车速度的3倍.若爸爸比小华早10分达到植物园,则从小华家到植物园的路程是30km.
周末,小华骑自行车从家出发到植物园游玩,从家出发0.5小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华离家1小时20分后,爸爸开车沿相同路线前往植物园.如图是他们离家的路程y(km)y与小华离家的时间x(h)的函数图象,已知爸爸开车的速度是小华骑车速度的3倍.若爸爸比小华早10分达到植物园,则从小华家到植物园的路程是30km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com