【题目】火锅是重庆的一张名片，深受广大市民的喜爱.重庆某火锅店采取堂食、外卖、店外摆摊（简称摆摊）三种方式经营，6月份该火锅店堂食、外卖、摆摊三种方式的营业额之比为3：5：2．随着促进消费政策的出台，该火锅店老板预计7月份总营业额会增加，其中摆摊增加的营业额占总增加的营业额的
，则摆摊的营业额将达到7月份总营业额的
，为使堂食、外卖7月份的营业额之比为8：5，则7月份外卖还需增加的营业额与7月份总营业额之比是__________．
科目：初中数学 来源： 题型：
【题目】如图，直线
交
轴于点A，交
轴于点B,抛物线
经过点A，交轴于点
，点P为直线AB下方抛物线上一动点，过点P作
于D，连接AP．
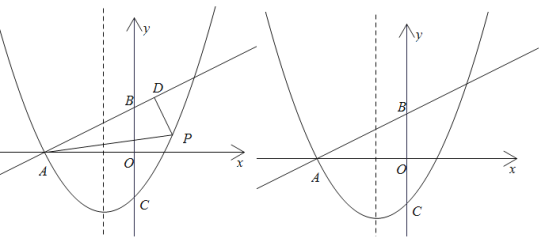
（1）求抛物线的解析式；
（2）若以点
为顶点的三角形与
相似，求点P的坐标；
（3）将绕点A旋转，当点O的对应点
落在抛物线的对称轴上时，请直接写出点B的对应点
的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知抛物线
：
的顶点为
，与
轴相交于点
，先将抛物线沿
轴翻折，再向右平移p个单位长度后得到抛物
，直线
；
经过，两点．
（1）求点的坐标，并结合图象直接写出不等式：
的解集；
（2）若抛物线的顶点
与点关于原点对称，求p的值及抛物线的解析式；
（3）若抛物线与轴的交点为
、
（点、分别与抛物线上点
、
对应），试问四边形
是何种特殊四边形？并说明其理由．
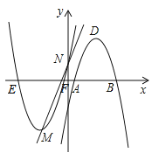
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】疫情防控，我们一直在坚守．某居委会组织两个检查组，分别对“居民体温”和“居民安全出行”的情况进行抽查．若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查，则他们恰好抽到同一个小区的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，已知抛物线
与直线AB相交于A，B两点，其中
，
．
（1）求该抛物线的函数表达式；
（2）点P为直线AB下方抛物线上的任意一点，连接PA，PB，求
面积的最大值；
（3）将该抛物线向右平移2个单位长度得到抛物线
，平移后的抛物线与原抛物线相交于点C，点D为原抛物线对称轴上的一点，在平面直角坐标系中是否存在点E，使以点B，C，D，E为顶点的四边形为菱形，若存在，请直接写出点E的坐标；若不存在，请说明理由．
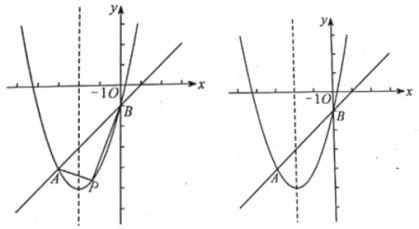
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在梯形
中，
，
，
，
．P为线段
上的一动点，且和B、C不重合，连接
，过点P作
交射线
于点E．
聪聪根据学习函数的经验，对这个问题进行了研究：
（1）通过推理，他发现
，请你帮他完成证明．
（2）利用几何画板，他改变的长度，运动点P，得到不同位置时，
、
的长度的对应值：
当
时，得表1：
| … | 1 | 2 | 3 | 4 | 5 | … |
| … | 0.83 | 1.33 | 1.50 | 1.33 | 0.83 | … |
当
时，得表2：
| … | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| … | 1.17 | 2.00 | 2.50 | 2.67 | 2.50 | 2.00 | 1.17 | … |
这说明，点P在线段上运动时，要保证点E总在线段上，
的长度应有一定的限制．
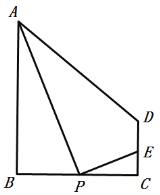
①填空：根据函数的定义，我们可以确定，在和的长度这两个变量中，_____的长度为自变量，_____的长度为因变量；
②设
，当点P在线段上运动时，点E总在线段上，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
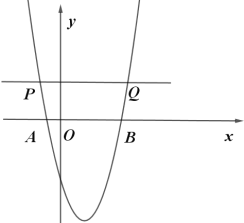
【题目】如图，已知二次函数y＝ax2＋bx－5（a，b是常数，a
0）的图象与x轴交于点A（－1，0）和点B（5，0）．动直线y＝t（t为常数）与抛物线交于不同的两点P、Q（点P在Q的左侧）．
（1）求抛物线的解析式；
（2）动直线y＝t与y轴交于点C，若CQ=3CP，求t的值；
（3）将抛物线y＝ax2＋bx－5在x轴下方的部分沿x轴翻折，若动直线y＝t与翻折后的图像交于点M、N，点M、N能否是线段PQ的三等分点？若能，求PQ的长度；若不能，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
