
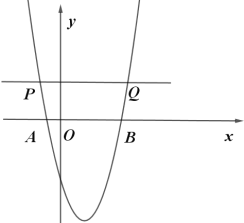
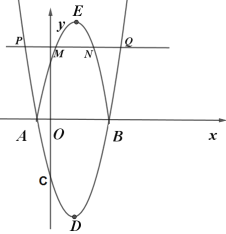
����Ŀ����ͼ����֪���κ���y��ax2��bx��5��a��b�dz�����a![]() 0����ͼ����x�ύ�ڵ�A����1��0���͵�B��5��0������ֱ��y��t��tΪ�������������߽��ڲ�ͬ������P��Q����P��Q����ࣩ��
0����ͼ����x�ύ�ڵ�A����1��0���͵�B��5��0������ֱ��y��t��tΪ�������������߽��ڲ�ͬ������P��Q����P��Q����ࣩ��
��1���������ߵĽ���ʽ��
��2����ֱ��y��t��y�ύ�ڵ�C����CQ=3CP����t��ֵ��
��3����������y��ax2��bx��5��x���·��IJ�����x�ᷭ�ۣ�����ֱ��y��t�뷭�ۺ��ͼ���ڵ�M��N����M��N�ܷ����߶�PQ�����ȷֵ㣿���ܣ���PQ�ij��ȣ������ܣ���˵�����ɣ�
���𰸡���1��![]() ����2��-8��7����3���ܣ�
����2��-8��7����3���ܣ�![]()
��������
��1������A����B��������������ߣ��ⷽ���鼴����������߽���ʽ��
��2����y��t��x����Ϸ�����x���·����ֽ������ۣ����������ߵĶԳ��Ժ�CQ=3CP���������P����Q�ĺ����꣬����Q��������������������t��ֵ��
��3�����ݶԳ��Կɵ÷��ۺ�������ߵĽ���ʽ���ٸ��ݵ�P����Q��ֱ��y=t��������![]() ����M����N��������
����M����N��������![]() �Ľ��㣬�������̣���õ�P��Q��M��N�����꣬�����õ�M��N���߶�PQ�����ȷֵ㣬�ó�PM=MN=NQ���ݴ����t��ֵ����������߶�PQ�ij���
�Ľ��㣬�������̣���õ�P��Q��M��N�����꣬�����õ�M��N���߶�PQ�����ȷֵ㣬�ó�PM=MN=NQ���ݴ����t��ֵ����������߶�PQ�ij���
�⣺��1����A����1��0����B��5��0�����������ϣ�
��![]() ����ã�
����ã�![]() ��
��
����κ�����ϵʽΪy��x2��4 x��5��
��2����y��t��x����Ϸ�����ͼ��
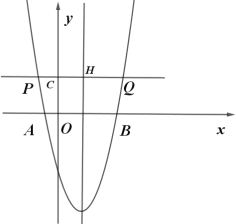
�����ߵĶԳ���![]() ����ֱ��y��t���ڵ�H��
����ֱ��y��t���ڵ�H��
��CH=2��
���������ߵĶԳ��Կɵã�PH=QH��
��CQ=3CP��
��PH=CH=2��QH=2CH=4��
��CQ=6��
���Q������Ϊ![]() ��
��
�ߵ�Q��������y��x2��4 x��5�ϣ�����ã�
![]() ��
��
��y��t��x����Ϸ�����ͼ��
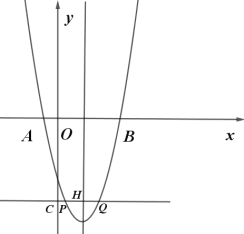
��ʱ�����������ߵĶԳ��Կɵã�
CH=HQ��
��CQ=3CP��
��CP=PH=1��HQ=2CP=2��
���P������Ϊ![]() ��
��
�ߵ�P��������y��x2��4 x��5�ϣ�����ã�
![]() ��
��
����������t��![]() ��7 ��
��7 ��
��3����M��N�������߶�PQ�����ȷֵ㣬��ʱ![]() ��
��
������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() ��
��
��������y��ax2��bx��5��x���·��IJ�����x�ᷭ�ۣ�
���E���D����x��Գƣ���E������Ϊ![]() ��
��
�෭�ۺ�������߽���ʽΪ��![]() ��
��
��ֱ��y=t��������![]() ����P��Q���㣬
����P��Q���㣬
��![]() ����ã�
����ã�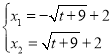 ��
��
���P������Ϊ![]() ����Q������Ϊ
����Q������Ϊ![]() ��
��
��ֱ��y=t��������![]() ����M��N���㣬
����M��N���㣬
��![]() ����ã�
����ã�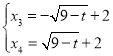 ,
,
���M������Ϊ![]() ����N������Ϊ
����N������Ϊ![]() ��
��
Ҫʹ��M��N���߶�PQ�����ȷֵ㣬��PM=MN=NQ��
![]() ��
��
��ã�![]() ��
��
��![]() ,
,



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һ����Ƭ�����ܹ�������ϲ��.����ij������ȡ��ʳ�������������̯����ư�̯�����ַ�ʽ��Ӫ��6�·ݸû������ʳ����������̯���ַ�ʽ��Ӫҵ��֮��Ϊ3��5��2�����Ŵٽ��������ߵij�̨���û�����ϰ�Ԥ��7�·���Ӫҵ������ӣ����а�̯���ӵ�Ӫҵ��ռ�����ӵ�Ӫҵ���![]() �����̯��Ӫҵ��ﵽ7�·���Ӫҵ���
�����̯��Ӫҵ��ﵽ7�·���Ӫҵ���![]() ��Ϊʹ��ʳ������7�·ݵ�Ӫҵ��֮��Ϊ8��5����7�·������������ӵ�Ӫҵ����7�·���Ӫҵ��֮����__________��
��Ϊʹ��ʳ������7�·ݵ�Ӫҵ��֮��Ϊ8��5����7�·������������ӵ�Ӫҵ����7�·���Ӫҵ��֮����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
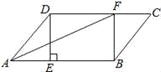
����Ŀ����ͼ����ABCD�У�����D��DE��AB�ڵ�E����F�ڱ�CD�ϣ�CF=AE������AF��BF.
(1)��֤���ı���BFDE�Ǿ��Σ�
(2)��֪��DAB=60�㣬AF�ǡ�DAB��ƽ���ߣ���AD=3����DC�ij���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ֱ��������ֽƬAOB��COD��ͼ1��ʾ���ã�ֱ�Ƕ����غ��ڵ�O����AB��13��CD��7������ֽƬAOB��������ֽƬCOD�Ƶ�O��ʱ����תa��0![]() ��
��![]() 90��������ͼ2��ʾ����BD��CD��ͬһֱ���ϣ���ͼ3��ʱ������ABC�����Ϊ____��
90��������ͼ2��ʾ����BD��CD��ͬһֱ���ϣ���ͼ3��ʱ������ABC�����Ϊ____��
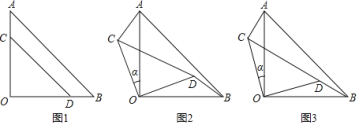
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��2��0����B��6��0������ABΪֱ������M������OF����M��E��F���㣬CΪ��AB���е㣬DΪEF���е㣮������OF��O����תʱ��CD����СֵΪ_____��
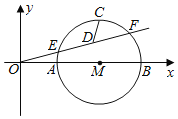
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+(4a��1)x��4��x�ύ�ڵ�A��B����y�ύ�ڵ�C����OC=2OB����DΪ�߶�OB��һ����(�����B�غ�)������D������DEFH����H��F���������ϣ���E��x���ϣ�
��1���������ߵĽ���ʽ��
��2��������DEFH���ܳ����ʱ�������DEFH�������
��3���ڣ�2���������£�����DEFH������������������x������ƽ��m����λ�������������DEFH�ı߽��ڵ�M��N������M��N����MNǡ��ƽ�־���DEFH���������m��ֵ��
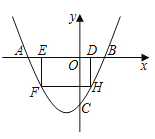
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊӭ��2020���35��ȫ��������Ƽ����´�����ijѧУ�ٰ���A�������ˣ�B����ģ��C���ƻû滭��D����Ϣѧ��E���Ƽ�С����������������ÿ���ޱ�һ�������������IJμ��������Ƴ���ͼ������������ͳ��ͼ��
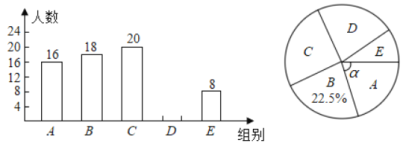
����ͳ��ͼ�е���Ϣ����������⣺
��1�����βμӱ�����ѧ��������_________����
��2��������ͳ��ͼ����������
��3��������ͳ��ͼ�б�ʾ�����˵�����Բ�Ľ�![]() �Ķ�����
�Ķ�����
��4����C���������3��ͬѧ��1������2��Ů������E���������3��ͬѧ��2������1��Ů�����У���ѡ1��ͬѧ�μ���һ��������������״ͼ���������ѡ����ͬѧ��ǡ����1������1��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com