
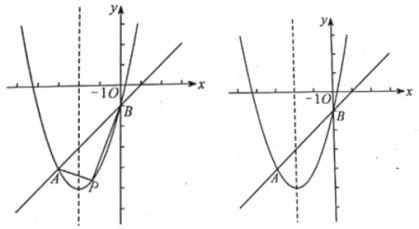
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯп![]() гыжБЯпABЯрНЛгкAЃЌBСНЕуЃЌЦфжа
гыжБЯпABЯрНЛгкAЃЌBСНЕуЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕуPЮЊжБЯпABЯТЗНХзЮяЯпЩЯЕФШЮвтвЛЕуЃЌСЌНгPAЃЌPBЃЌЧѓ![]() УцЛ§ЕФзюДѓжЕЃЛ
УцЛ§ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉНЋИУХзЮяЯпЯђгвЦНвЦ2ИіЕЅЮЛГЄЖШЕУЕНХзЮяЯп![]() ЃЌЦНвЦКѓЕФХзЮяЯпгыдХзЮяЯпЯрНЛгкЕуCЃЌЕуDЮЊдХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЌдкЦНУцжБНЧзјБъЯЕжаЪЧЗёДцдкЕуEЃЌЪЙвдЕуBЃЌCЃЌDЃЌEЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕуEЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЌЦНвЦКѓЕФХзЮяЯпгыдХзЮяЯпЯрНЛгкЕуCЃЌЕуDЮЊдХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЌдкЦНУцжБНЧзјБъЯЕжаЪЧЗёДцдкЕуEЃЌЪЙвдЕуBЃЌCЃЌDЃЌEЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕуEЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() УцЛ§зюДѓжЕЮЊ
УцЛ§зюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉДцдкЃЌ
ЃЛЃЈ3ЃЉДцдкЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуAЁЂBЕФзјБъДњШыХзЮяЯпБэДяЪНЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЩш![]() ЃЌЧѓЕУНтЮіЪНЃЌЙ§ЕуPзїxжсЕУДЙЯпгыжБЯпABНЛгкЕуFЃЌЩшЕу
ЃЌЧѓЕУНтЮіЪНЃЌЙ§ЕуPзїxжсЕУДЙЯпгыжБЯпABНЛгкЕуFЃЌЩшЕу![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]()
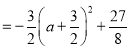 ЃЌМДПЩЧѓНтЃЛ
ЃЌМДПЩЧѓНтЃЛ
ЃЈ3ЃЉЗжBCЮЊСтаЮЕФБпЁЂСтаЮЕФЕФЖдНЧЯпСНжжЧщПіЃЌЗжБ№ЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉЁпХзЮяЯпЙ§![]() ЃЌ
ЃЌ![]()
Ёр![]()
Ёр![]()
Ёр![]()
ЃЈ2ЃЉЩш![]() ЃЌНЋЕу
ЃЌНЋЕу![]()
![]() ДњШы
ДњШы![]()
Ёр![]()
Й§ЕуPзїxжсЕУДЙЯпгыжБЯпABНЛгкЕуF
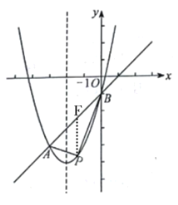
ЩшЕу![]() ЃЌдђ
ЃЌдђ![]()
гЩЧІДЙЖЈРэПЩЕУ
![]()
![]()
![]()
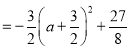
Ёр![]() УцЛ§зюДѓжЕЮЊ
УцЛ§зюДѓжЕЮЊ![]()
ЃЈ3ЃЉЃЈ3ЃЉХзЮяЯпЕФБэДяЪНЮЊЃКyЃНx2ЃЋ4x1ЃНЃЈxЃЋ2ЃЉ25ЃЌ
дђЦНвЦКѓЕФХзЮяЯпБэДяЪНЮЊЃКyЃНx25ЃЌ
СЊСЂЩЯЪіСНЪНВЂНтЕУЃК![]() ЃЌЙЪЕуCЃЈ1ЃЌ4ЃЉЃЛ
ЃЌЙЪЕуCЃЈ1ЃЌ4ЃЉЃЛ
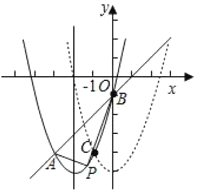
ЩшЕуDЃЈ2ЃЌmЃЉЁЂЕуEЃЈsЃЌtЃЉЃЌЖјЕуBЁЂCЕФзјБъЗжБ№ЮЊЃЈ0ЃЌ1ЃЉЁЂЃЈ1ЃЌ4ЃЉЃЛ
ЂйЕБBCЮЊСтаЮЕФБпЪБЃЌ
ЕуCЯђгвЦНвЦ1ИіЕЅЮЛЯђЩЯЦНвЦ3ИіЕЅЮЛЕУЕНBЃЌЭЌбљDЃЈEЃЉЯђгвЦНвЦ1ИіЕЅЮЛЯђЩЯЦНвЦ3ИіЕЅЮЛЕУЕНEЃЈDЃЉЃЌ
МД2ЃЋ1ЃНsЧвmЃЋ3ЃНtЂйЛђ21ЃНsЧвm3ЃНtЂкЃЌ
ЕБЕуDдкEЕФЯТЗНЪБЃЌдђBEЃНBCЃЌМДs2ЃЋЃЈtЃЋ1ЃЉ2ЃН12ЃЋ32ЂлЃЌ
ЕБЕуDдкEЕФЩЯЗНЪБЃЌдђBDЃНBCЃЌМД22ЃЋЃЈmЃЋ1ЃЉ2ЃН12ЃЋ32ЂмЃЌ
СЊСЂЂйЂлВЂНтЕУЃКsЃН1ЃЌtЃН2Лђ4ЃЈЩсШЅ4ЃЉЃЌЙЪЕуEЃЈ1ЃЌ2ЃЉЃЛ
СЊСЂЂкЂмВЂНтЕУЃКsЃН-3ЃЌtЃН-4ЁР![]() ЃЌЙЪЕуEЃЈ-3ЃЌ-4ЃЋ
ЃЌЙЪЕуEЃЈ-3ЃЌ-4ЃЋ![]() ЃЉЛђЃЈ-3ЃЌ-4
ЃЉЛђЃЈ-3ЃЌ-4![]() ЃЉЃЛ
ЃЉЃЛ
ЂкЕБBCЮЊСтаЮЕФЕФЖдНЧЯпЪБЃЌ
дђгЩжаЕуЙЋЪНЕУЃК1ЃНs2Чв41ЃНmЃЋtЂнЃЌ
ДЫЪБЃЌBDЃНBEЃЌМД22ЃЋЃЈmЃЋ1ЃЉ2ЃНs2ЃЋЃЈtЃЋ1ЃЉ2ЂоЃЌ
СЊСЂЂнЂоВЂНтЕУЃКsЃН1ЃЌtЃН3ЃЌ
ЙЪЕуEЃЈ1ЃЌ3ЃЉЃЌ
злЩЯЃЌЕуEЕФзјБъЮЊЃКЃЈ1ЃЌ2ЃЉЛђ![]() Лђ
Лђ![]() ЛђЃЈ1ЃЌ3ЃЉЃЎ
ЛђЃЈ1ЃЌ3ЃЉЃЎ
ЁрДцдкЃЌ![]()


 ПкЫуЬтЬьЬьСЗЯЕСаД№АИ
ПкЫуЬтЬьЬьСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНМвЩЬГЁЦНЪБвдЭЌбљМлИёГіЪлЯрЭЌЕФЩЬЦЗЃЌаТЙквпЧщЦкМфЃЌЮЊСЫМѕЩйПтДцЃЌМзЁЂввСНМвЩЬГЁДђелДйЯњЃЌМзЩЬГЁЫљгаЩЬЦЗАД9елГіЪлЃЌввЩЬГЁЖдвЛДЮЙКЮяжаГЌЙ§100дЊКѓЕФМлИёВПЗжДђ8елЃЎ
ЂХ.вд![]() ЃЈЕЅЮЛЃКдЊЃЉБэЪОЩЬЦЗдМлЃЌ
ЃЈЕЅЮЛЃКдЊЃЉБэЪОЩЬЦЗдМлЃЌ![]() ЃЈЕЅЮЛЃКдЊЃЉБэЪОЪЕМЪЙКЮяН№ЖюЃЌЗжБ№ОЭСНМвЩЬГЁЕФШУРћЗНЪНаДГі
ЃЈЕЅЮЛЃКдЊЃЉБэЪОЪЕМЪЙКЮяН№ЖюЃЌЗжБ№ОЭСНМвЩЬГЁЕФШУРћЗНЪНаДГі![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂЦ.аТЙквпЧщЦкМфШчКЮбЁдёетСНМвЩЬГЁШЅЙКЮяИќЪЁЧЎЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Љx2+bx+cКЭжБЯпy=x+1НЛгкAЃЌBСНЕуЃЌЕуAдкxжсЩЯЃЌЕуBдкжБЯпx=3ЩЯЃЌжБЯпx=3гыxжсНЛгкЕуC

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPДгЕуAГіЗЂЃЌвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШбиЯпЖЮABЯђЕуBдЫЖЏЃЌЕуQДгЕуCГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиЯпЖЮCAЯђЕуAдЫЖЏЃЌЕуPЃЌQЭЌЪБГіЗЂЃЌЕБЦфжавЛЕуЕНДяжеЕуЪБЃЌСэвЛИіЕувВЫцжЎЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЈtЃО0ЃЉЃЎвдPQЮЊБпзїОиаЮPQNMЃЌЪЙЕуNдкжБЯпx=3ЩЯЃЎ
ИіЕЅЮЛГЄЖШЕФЫйЖШбиЯпЖЮABЯђЕуBдЫЖЏЃЌЕуQДгЕуCГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиЯпЖЮCAЯђЕуAдЫЖЏЃЌЕуPЃЌQЭЌЪБГіЗЂЃЌЕБЦфжавЛЕуЕНДяжеЕуЪБЃЌСэвЛИіЕувВЫцжЎЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЈtЃО0ЃЉЃЎвдPQЮЊБпзїОиаЮPQNMЃЌЪЙЕуNдкжБЯпx=3ЩЯЃЎ
ЂйЕБtЮЊКЮжЕЪБЃЌОиаЮPQNMЕФУцЛ§зюаЁЃПВЂЧѓГізюаЁУцЛ§ЃЛ
ЂкжБНгаДГіЕБtЮЊКЮжЕЪБЃЌЧЁКУгаОиаЮPQNMЕФЖЅЕуТфдкХзЮяЯпЩЯЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=kx+bЕФЭМЯѓгыxжсНЛгкЕуBЃЈ6,0ЃЉЃЌгыyжсНЛгкЕуAЃЌгыЖўДЮКЏЪ§y=ax2ЕФЭМЯѓдкЕквЛЯѓЯоФкНЛгкЕуCЃЈ3,3ЃЉЃЎ

(1)ЧѓДЫвЛДЮКЏЪ§гыЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
(2)ШєЕуDдкЯпЖЮACЩЯЃЌгыyжсЦНааЕФжБЯпDEгыЖўДЮКЏЪ§ЭМЯѓЯрНЛгкЕуEЃЌЁЯADO=ЁЯOEDЃЌЧѓЕуDзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЛ№ЙјЪЧжиЧьЕФвЛеХУћЦЌЃЌЩюЪмЙуДѓЪаУёЕФЯВАЎ.жиЧьФГЛ№ЙјЕъВЩШЁЬУЪГЁЂЭтТєЁЂЕъЭтАкЬЏЃЈМђГЦАкЬЏЃЉШ§жжЗНЪНОгЊЃЌ6дТЗнИУЛ№ЙјЕъЬУЪГЁЂЭтТєЁЂАкЬЏШ§жжЗНЪНЕФгЊвЕЖюжЎБШЮЊ3ЃК5ЃК2ЃЎЫцзХДйНјЯћЗбеўВпЕФГіЬЈЃЌИУЛ№ЙјЕъРЯАхдЄМЦ7дТЗнзмгЊвЕЖюЛсдіМгЃЌЦфжаАкЬЏдіМгЕФгЊвЕЖюеМзмдіМгЕФгЊвЕЖюЕФ![]() ЃЌдђАкЬЏЕФгЊвЕЖюНЋДяЕН7дТЗнзмгЊвЕЖюЕФ
ЃЌдђАкЬЏЕФгЊвЕЖюНЋДяЕН7дТЗнзмгЊвЕЖюЕФ![]() ЃЌЮЊЪЙЬУЪГЁЂЭтТє7дТЗнЕФгЊвЕЖюжЎБШЮЊ8ЃК5ЃЌдђ7дТЗнЭтТєЛЙашдіМгЕФгЊвЕЖюгы7дТЗнзмгЊвЕЖюжЎБШЪЧ__________ЃЎ
ЃЌЮЊЪЙЬУЪГЁЂЭтТє7дТЗнЕФгЊвЕЖюжЎБШЮЊ8ЃК5ЃЌдђ7дТЗнЭтТєЛЙашдіМгЕФгЊвЕЖюгы7дТЗнзмгЊвЕЖюжЎБШЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌDЁЂEЗжБ№ЪЧБп
ЃЌDЁЂEЗжБ№ЪЧБп![]() ЁЂ
ЁЂ![]() ЕФжаЕуЃЎНЋ
ЕФжаЕуЃЎНЋ![]() ШЦЕуEа§зЊ180ЖШЃЌЕУ
ШЦЕуEа§зЊ180ЖШЃЌЕУ![]() ЃЎ
ЃЎ
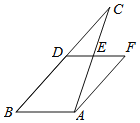
ЃЈ1ЃЉХаЖЯЫФБпаЮ![]() ЕФаЮзДЃЌВЂжЄУїЃЛ
ЕФаЮзДЃЌВЂжЄУїЃЛ
ЃЈ2ЃЉвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌЧѓЫФБпаЮ
ЃЌЧѓЫФБпаЮ![]() ЕФУцЛ§SЃЎ
ЕФУцЛ§SЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
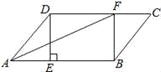
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌЙ§ЕуDзїDEЁЭABгкЕуEЃЌЕуFдкБпCDЩЯЃЌCF=AEЃЌСЌНгAFЃЌBF.
(1)ЧѓжЄЃКЫФБпаЮBFDEЪЧОиаЮЃЛ
(2)вбжЊЁЯDAB=60ЁуЃЌAFЪЧЁЯDABЕФЦНЗжЯпЃЌШєAD=3ЃЌЧѓDCЕФГЄЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
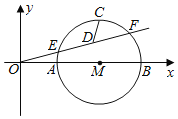
ЁОЬтФПЁПШчЭМЃЌAЃЈ2ЃЌ0ЃЉЁЂBЃЈ6ЃЌ0ЃЉЃЌвдABЮЊжБОЖзїЁбMЃЌЩфЯпOFНЛЁбMгкEЁЂFСНЕуЃЌCЮЊЛЁABЕФжаЕуЃЌDЮЊEFЕФжаЕуЃЎЕБЩфЯпOFШЦOЕуа§зЊЪБЃЌCDЕФзюаЁжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃгыЭМЪщЙндкЭЌвЛЬѕБЪжБЕРТЗЩЯЃЌМзДгбЇаЃШЅЭМЪщЙнЃЌввДгЭМЪщЙнЛибЇаЃЃЌМзЁЂввСНШЫЖМдШЫйВНааЧвЭЌЪБГіЗЂЃЌввЯШЕНДяФПЕФЕи.СНШЫжЎМфЕФОрРыyЃЈУзЃЉгыЪБМфtЃЈЗжжгЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪО.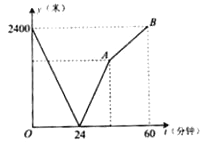
ЃЈ1ЃЉИљОнЭМЯѓаХЯЂЃЌЕБt=________ЗжжгЪБМзввСНШЫЯргіЃЌМзЕФЫйЖШЮЊ________Уз/ЗжжгЃЛ
ЃЈ2ЃЉЧѓГіЯпЖЮABЫљБэЪОЕФКЏЪ§БэДяЪН.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com