
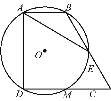
【题目】如图,直角梯形ABCD中,∠BAD=∠CDA=90°,AB=![]() ,CD=2
,CD=2![]() ,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2
,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2![]() ;④AE=
;④AE=![]() .其中正确的结论是( )
.其中正确的结论是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【答案】B
【解析】
连接BD,BM,AM,EM,DE,利用三个角为直角的四边形为矩形得到ABMD为矩形,利用矩形的对边相等得到AB=DM,进而可证明DM=CM,故选项①正确;在Rt△DEC中,由M为CD的中点,利用斜边上的中线等于斜边的一半得到DM与EM相等,从而AB=EM,所以弧AB=弧EM,故选项②正确;先证明四边形AMCB为平行四边形,可得出AM=BC,等量代换得到BC=BD,由BD为圆的直径,可得△DEC为直角三角形,利用勾股定理可求出DE的长,设BE=x,则BD=BC=BE+EC=x+2,在Rt△BDE中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出BC的长,即为BD的长,确定出圆的直径,即可对于选项③作出判断;在Rt△AEM中,由AM与ME的长,利用勾股定理求出AE的长,即可对于选项④作出判断.
连接BD,BM,AM,EM,DE,
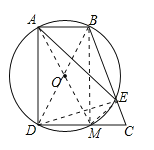
∵∠BAD=90°,
∴BD为圆的直径,
∴∠BMD=90°,
∴∠BAD=∠CDA=∠BMD=90°,
∴四边形ABMD矩形,
∴AB=DM,
又∵CD=2AB,
∴CD=2DM,即DM=MC;
故选项①正确;
在Rt△DEC中,M是DC中点,
∴EM=DM=![]() CD=
CD=![]() ,
,
∴弧EM=弧DM,
又∵AB=DM,
∴弧AB=弧DM,
∴弧AB=弧EM,
故选项②正确;
∵AB∥MC,AB=MC,
∴四边形ABCM是平行四边形,
∴AM=BC,又BD=AM,
∴BD=BC,
∵BD是直径,
∴∠BED=90°,即∠DEC=90°,
又EC=2,DC=2![]() ,
,
根据勾股定理得:DE=![]() =2
=2![]() ,
,
设BE=x,BD=BC=BE+EC=x+2,
在Rt△BDE中,根据勾股定理得:BE2+DE2=BD2,即x2+20=(x+2)2,
解得:x=4,
∴BD=6,故选项③错误;
在Rt△AEM中,AM=6,EM=![]() ,
,
根据勾股定理得:AE=![]() =
=![]() ;
;
故选项④正确;
则正确的选项为:①②④.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=6.将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( )
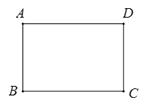
A. 6 B. 3 C. 2.5 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知不在同一条直线上的三点![]() 、
、![]() 、
、![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)按下列要求作图(用尺规作图,保留作图痕迹)

①作射线![]() ;
;
②在线段![]() 上截取
上截取![]() ;
;
③在线段![]() 上截取
上截取![]() .
.
恭喜您!通过刚才的动手操作画图,你作出了闻名世界的“黄金分割点”.像这样点![]() 就称为线段
就称为线段![]() 的“黄金分割点”.
的“黄金分割点”.
(2)阅读下面材料,并完成相关问题;
黄金分割点是指把一条线段分割为两部分,使其中一部分的长约是全长的0.618倍,则称这个点为黄金分割点.如图,![]() 为线段
为线段![]() 上一点,如果
上一点,如果![]() ,那么点
,那么点![]() 为线段
为线段![]() 的黄金分割点.
的黄金分割点.
![]()
已知某舞台的宽为30米,一次演出时两位主持人分别站在舞台![]() 上的两个黄金分割点
上的两个黄金分割点![]() 和
和![]() 处,如图,则这两位主持人之间的距离
处,如图,则这两位主持人之间的距离![]() 约为_________米.
约为_________米.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
(1)元旦期间,“茂业“商场对某品牌羽绒服实行七折销售,张阿姨到该商场购买了一件该品牌的羽绒服发现比不打折时可省下240元,那么该品牌的标价是多少元?
(2)某公司共有工人40人,已知一个工人每小时可制造10个![]() 种零件或20个
种零件或20个![]() 种零件,每个工人能而且只能制造其中的一种零件.
种零件,每个工人能而且只能制造其中的一种零件.
①如果这些工人每小时能制造![]() 、
、![]() 两种零件共550个,请问其中参加制造
两种零件共550个,请问其中参加制造![]() 种零件的工人有多少人?
种零件的工人有多少人?
②如果1个![]() 种零件与3个
种零件与3个![]() 种零件组合后能形成一个整件,为使这些工人每小时制造出的零件都能恰好组合成整件,那么应安排多少工人制造
种零件组合后能形成一个整件,为使这些工人每小时制造出的零件都能恰好组合成整件,那么应安排多少工人制造![]() 种零件?
种零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前,安徽黄山脚下的小村庄的集市上,人山人海,还有人在摆“摸彩”游戏,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1~20号)和1只红球,规定:每次只摸一只球.摸前交1元钱且在1~20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元.
(1)你认为该游戏对“摸彩”者有利吗?说明你的理由.
(2)若一个“摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
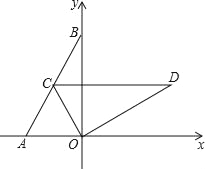
【题目】已知如图,在直角坐标系xOy中,点A,点B坐标分别为(﹣1,0),(0,![]() ),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
(1)求点C的坐标;
(2)△AOB绕点O顺时针旋转60°所扫过的面积;
(3)线段AB绕点O顺时针旋转60°所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
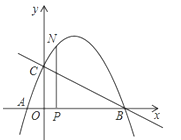
【题目】如图,抛物线与x轴交于点A(﹣![]() , 0),点B(2,0),与y轴交于点C(0,1),连接BC.
, 0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣![]() <t<2),求△ABN的面积s与t的函数解析式;
<t<2),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com