
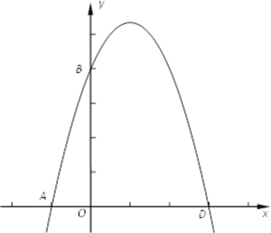
【题目】如图,在平面直角坐标系中,己知二次函数![]() 的图像与y轴交于点B(0, 4),与x轴交于点A(-1,0)和点D.
的图像与y轴交于点B(0, 4),与x轴交于点A(-1,0)和点D.
(1)求二次函数的解析式;
(2)求抛物线的顶点和点D的坐标;
(3)在抛物线上是否存在点P,使得△BOP的面积等于![]() ?如果存在,请求出点P的坐标?如果不存在,请说明理由.
?如果存在,请求出点P的坐标?如果不存在,请说明理由.
【答案】(1)![]() ;(2)D的坐标为(3,0),顶点坐标为(1,
;(2)D的坐标为(3,0),顶点坐标为(1,![]() );(3)满足条件的点P有两个,坐标分别为P1(
);(3)满足条件的点P有两个,坐标分别为P1(![]() ,
,![]() )、P2(
)、P2(![]() ).
).
【解析】
(1)利用待定系数法求出二次函数解析式即可;
(2)根据二次函数的解析式得点D的坐标,将解析式化为顶点式可得顶点的坐标;
(3)设P的坐标为P(x,y),到y轴的距离为|x|,则S△BOP=![]() BO|x|,解出x=±
BO|x|,解出x=±![]() ,进而得出P点坐标.
,进而得出P点坐标.
解:(1)把点A(-1,0)和点B(0, 4)代入二次函数![]() 中得:
中得:
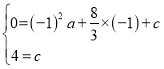
解得: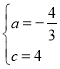
所以二次函数的解析式为:![]() ;
;
(2)根据(1)得点D的坐标为(3,0),
![]() =
=![]() ,
,
∴顶点坐标为(1,![]() );
);
(3)存在这样的点P,设P的坐标为P(x,y),到y轴的距离为∣x∣
∵ S△BOP=![]() BO∣x∣
BO∣x∣
∴![]() =
=![]() ×4∣x∣
×4∣x∣
解得:∣x∣=![]() 所以x=±
所以x=±![]()
把x=![]() 代入
代入![]() 中得:
中得:
![]()
即:y=![]() ,
,
把x=-![]() 代入
代入![]() 中得:
中得:
![]()
即:y=-![]()
∴满足条件的点P有两个,坐标分别为P1(![]() ,
,![]() )、P2(
)、P2(![]() ).
).


科目:初中数学 来源: 题型:
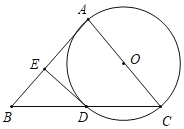
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC相交于点D,过点D作⊙O的切线与AB相交于点E.
(1)求证:DE⊥AB;
(2)若BE=2,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,BE⊥CD于点E,DF⊥BC于点F.
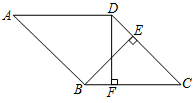
(1)求证:BF=DE;
(2)分别延长BE和AD,交于点G,若∠A=45°,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
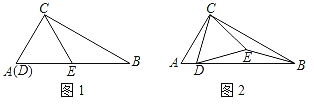
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,点D在AB边上,△CDE是等边三角形.
(1)如图1,当点E在AB边上时,CE与BE有何数量关系,请说明理由;
(2)如图2,当点E在△ABC内时,猜想CE与BE的数量关系,并加以证明;
(3)再另画一种情况,写出相应结论.(不用证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
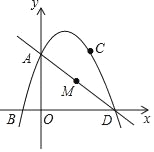
【题目】如图,抛物线y=ax2+bx+3经过点 B(﹣1,0),C(2,3),抛物线与y轴的焦点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t.
(1)求抛物线的表达式;
(2)过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)
(3)在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;
(4)在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
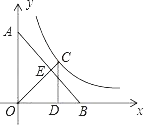
【题目】如图,点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,连接OE并延长交反比例函数y=![]() (x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则OE﹣EC=_____.
(x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则OE﹣EC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年伊始,一场突如其来的疫情防控战在中华大地骤然打响,全国人民自觉居家减少外出,师生停课不停学,举国共抗疫情.某中学在复学后,为了了解学生们在居家期间的生活状态,以更好地保护复学后学生们的身心健康,对本校学生进行了“居家期间学习之余主要活动”的抽样调查.种类为:(A)强身健体、(B)艺术熏陶、(C)经典阅读、(D)分担劳动、(E)其他.针对以上活动种类,统计学生们花时间最多的种类的人数,以绘制成如下两幅不完整的条形统计图和扇形统计图.
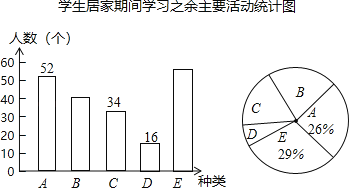
请根据图中的信息,回答下列问题.
(1)被抽样调查的总人数为 人;
(2)补全条形统计图;
(3)若该校共有学生1800人,请估算种类D的大约人数;
(4)据此疫情经历,给自己提出一条人生建议 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABE中,∠B=90°,AB=BE,将△ABE绕点A逆时针旋转45°,得到△AHD,过D作DC⊥BE交BE的延长线于点C,连接BH并延长交DC于点F,连接DE交BF于点O.下列结论:①DE平分∠HDC;②DO=OE;③H是BF的中点;④BC-CF=2CE;⑤CD=HF,其中正确的有( )
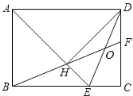
A.5个B.4个C.3个D.2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com