
分析 由中线长可得斜边长,根据周长已知,可列出另外两边的方程,再根据勾股定理列出另一个方程,联立解得两直角边长.
解答 解:设两直角边长分别为x,y;
∵直角三角形斜边上的中线长为1,
∴斜边长为2.
周长为2+$\sqrt{6}$=x+y+2,得x+y=$\sqrt{6}$.①
由勾股定理得$\sqrt{{x}^{2}+{y}^{2}}$.②
①②联立解得x=$\frac{\sqrt{6}-\sqrt{2}}{2}$,y=$\frac{\sqrt{6}+\sqrt{2}}{2}$,
所以这个直角三角形的三边长为$\frac{\sqrt{6}-\sqrt{2}}{2}$,$\frac{\sqrt{6}+\sqrt{2}}{2}$,2.
点评 此题考查二次根式的实际运用,勾股定理的运用,利用周长和勾股定理联立方程是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
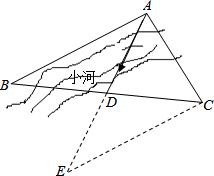 如图,在河的北岸种植一排小树AB,点C在河的南岸,已知在△ABC中,D是BC边的中点,AD的长度和方向都已确定,现在想要过点C也种植一排与AB平行的小树,小明使用了如下方法:延长AD到E,使DE=DA,连接 EC,那么就能得知AB∥EC,请你说明这样做的理由.
如图,在河的北岸种植一排小树AB,点C在河的南岸,已知在△ABC中,D是BC边的中点,AD的长度和方向都已确定,现在想要过点C也种植一排与AB平行的小树,小明使用了如下方法:延长AD到E,使DE=DA,连接 EC,那么就能得知AB∥EC,请你说明这样做的理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com