Question

7．我们知道，三角形的中线平分三角形的面积．
（1）AE 是△AEC的中线．在△ABC的外部作△ACD，F是AD的中点，连接CF（图1），若四边形ABCD的面积是S，则四边形AECF的面积是$\frac{S}{2}$．
（2）任意四边形ABCD的面积是S，E、F分别是一组对边AB、CD的中点，连接AF、CE（图2），则四边形AECF的面积是$\frac{S}{2}$．
（3）四边形ABCD的面积是10，E，F分别是一组对边AB，CD上的点，且AE=$\frac{1}{3}$AB，CF=$\frac{1}{3}$CD，连接AF，CE（图3），则四边形AECF的面积是$\frac{10}{3}$．
（4）若八边形ABCDEFGH的面积是10，K，M，N，O，P，Q分别是AB，BC，CD，EF，FG，GH的中点，连接KH，MG，NF，OD，PC，QB（图4），则图中阴影部分的面积是5．

Answer 1

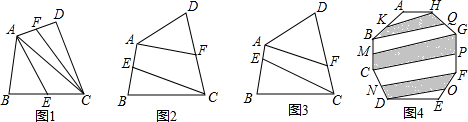
分析 （1）分别可得S_△AEC=$\frac{1}{2}$S_△ABC，S_△AFC=$\frac{1}{2}$S_△ACD，从而可得S_{四边形AECF}=$\frac{1}{2}$S_{四边形ABCD}．
（2）同（1），可得S_{四边形AECF}=$\frac{1}{2}$S_{四边形ABCD}．
（3）分别得到S_△AEC=$\frac{1}{3}$S_△ABC，S_△AFC=$\frac{1}{3}$S_△ACD，从而可得S_{四边形AECF}=$\frac{1}{3}$S_{四边形ABCD}．
（4）连接CF、BG，根据（2）的结论，可得答案．

解答 解：（1）∵AE是△AEC的中线，
∴CE=$\frac{1}{2}$BC，
∴S_△AEC=$\frac{1}{2}$S_△ABC，
同理：S_△AFC=$\frac{1}{2}$S_△ACD，
∴S_{四边形AECF}=$\frac{1}{2}$S_{四边形ABCD}=$\frac{S}{2}$．

（2）连接AC，如图a：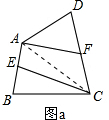

则S_{四边形AECF}=$\frac{1}{2}$S_{四边形ABCD}=$\frac{S}{2}$．

（3）连接AC，如图b：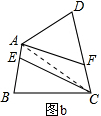

∵AE=$\frac{1}{3}$AB，CF=$\frac{1}{3}$CD，
∴S_△AEC=$\frac{1}{3}$S_△ABC，S_△AFC=$\frac{1}{3}$S_△ACD，
∴S_{四边形AECF}=$\frac{1}{3}$S_{四边形ABCD}=$\frac{10}{3}$．
（4）连接CF、BG，如图c：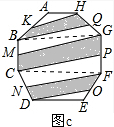

则可得S_{四边形KBQH}=$\frac{1}{2}$S_{四边形ABGH}，S_{四边形MCPG}=$\frac{1}{2}$S_{四边形BCFG}，S_{四边形NDOF}=$\frac{1}{2}$S_{四边形CDEF}，
∴S阴影=$\frac{1}{2}$S_{八边形ABCDEFGH}=5．
故答案为：$\frac{S}{2}$、$\frac{S}{2}$、$\frac{10}{3}$、5．

点评 本题考查了四边形的综合，解答本题的关键是掌握三角形中线的性质，注意融会贯通，将前面的结论运用到后面的解题中去，难度一般．