
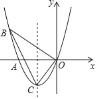
【题目】如图,已知抛物线y=ax2+bx经过点A(﹣2,0)、B(﹣3,3),顶点为C.
(1)求抛物线的函数表达式;
(2)若点P是第一象限内的抛物线上一动点,过点P作PM⊥x轴于点M,则是否存在点P,使得以P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1) y=x2+2x;(2)见解析.
【解析】
(1)利用待定系数法直接求出抛物线的解析式;(2)分两种情况讨论,①若△AMP∽△BOC,②若△PMA∽△BOC,根据相似三角形对应边的比相等可以求出P点坐标.
解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),且过A(﹣2,0),B(﹣3,3),O(0,0)可得
![]() ,
,
解得:![]() .
.
故抛物线的解析式为:y=x2+2x;
(2)存在,
如图:∵B(﹣3,3),C(﹣1,﹣1),根据勾股定理得:
BO2=18,CO2=2,BC2=20,
∴BO2+CO2=BC2.
∴△BOC是直角三角形.
假设存在点P,使以P,M,A为顶点的 三角形与△BOC相似,
设P(x,y),由题意知x>0,y>0,且y=x2+2x,
①若△AMP∽△BOC,则![]() =
=![]() ,
,
即 x+2=3(x2+2x)
得:x1=![]() ,x2=﹣2(舍去).
,x2=﹣2(舍去).
当x=![]() 时,y=
时,y=![]() ,即P(
,即P(![]() ,
,![]() ).
).
②若△PMA∽△BOC,则![]() =
=![]() ,
,
即:x2+2x=3(x+2)
得:x1=3,x2=﹣2(舍去)
当x=3时,y=15,即P(3,15).
故符合条件的点P有两个,分别是P(![]() ,
,![]() )和(3,15).
)和(3,15).


科目:初中数学 来源: 题型:
【题目】已知点P的坐标为(-3,4),作出点P关于x轴对称的点P1,称为第1次变换;再作出点P1关于y轴对称的点P2,称为第2次变换;再作点P2关于x轴对称的点P3,称为第3次变换,…,依次类推,则第2019次变换得到的点P2019的坐标为 ____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=10厘米,BC=6厘米,点P沿AB边从点A开始向点B以3厘米/秒的速度移动;点Q沿DA边从点D开始向点A以2厘米/秒的速度移动.如果P、Q同时出发,用t (秒)表示移动的时间,那么:
(1)如图1,用含t的代数式表示AP= ,AQ= .并求出当t为何值时线段AP=AQ.
(2)如图2,在不考虑点P的情况下,连接QB,问:当t为何值时△QAB的面积等于长方形面积的![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=![]() x相交于点A.
x相交于点A.
(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
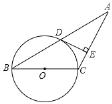
【题目】如图,在△ABC中,∠A=30°,AC=BC,以BC为直径的⊙O与边AB交于点D,过D作DE⊥AC于E.
(1)证明:DE为⊙O的切线.
(2)若⊙O的半径为2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.求A,B两点间的距离(结果精确到0.1km).
(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在自习课上,小明拿来如下框的一道题目(原问题)和合作学习小组的同学们交流.
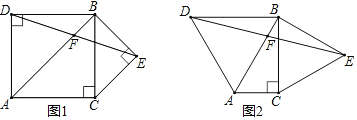
如图1,已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB,BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F.探究线段DF与EF的数量关系.
小红同学的思路是:过点D作DG⊥AB于点G,构造全等三角形,通过推理使问题得解.
小华同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.
请你参考小明同学的思路,探究并解决以下问题:
(1)写出原问题中DF与EF的数量关系为 .
(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com