
【题目】为测量被荷花池相隔的两树![]() 、
、![]() 的距离,数学活动小组设计了如图所示的测量方案:在
的距离,数学活动小组设计了如图所示的测量方案:在![]() 的垂线
的垂线![]() 上取两点
上取两点![]() 、
、![]() ,再定出
,再定出![]() 的垂线
的垂线![]() ,使
,使![]() 、
、![]() 、
、![]() 在一条直线上.其中三位同学分别测量出了三组数据:
在一条直线上.其中三位同学分别测量出了三组数据:
![]() 、
、![]() ;
;
![]() 、
、![]() ;
;
![]() 、
、![]() 、
、![]() .
.
能根据所测数据,求得![]() 、
、![]() 两树距离的是( )
两树距离的是( )

A. (1) B. (1),(2) C. (2),(3) D. (1),(3)
科目:初中数学 来源: 题型:
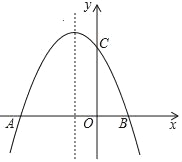
【题目】抛物线y=﹣x2+bx+c与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)在抛物线上求一点P,使S△PAB=S△ABC,写出P点的坐标;
(3)在抛物线的对称轴上是否存在点Q,使得△QBC的周长最小?若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是2018年三月份某居民小区随机抽取20户居民的用水情况:
月用水量/吨 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
户数 | 2 | 4 | m | 4 | 3 | 0 | 1 |
(1)求出m= ,补充画出这20户家庭三月份用电量的条形统计图;
(2)据上表中有关信息,计算或找出下表中的统计量,并将结果填入表中:
统计量名称 | 众数 | 中位数 | 平均数 |
数据 |
|
|
|
(3)为了倡导“节约用水,绿色环保”的意识,江赣市自来水公司实行“梯级用水、分类计费”,价格表如下:
月用水梯级标准 | Ⅰ级(30吨以内) | Ⅱ级(超过30吨的部分) |
单价(元/吨) | 2.4 | 4 |
如果该小区有500户家庭,根据以上数据,请估算该小区三月份有多少户家庭达到Ⅱ级标准?并估算这些Ⅱ级用水户的总水费是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将![]() 化为分数形式
化为分数形式
由于![]() =0.777…,设x=0.777…①
=0.777…,设x=0.777…①
则10x=7.777…②
②﹣①得9x=7,解得x=![]() ,于是得
,于是得![]() =
=![]() .
.
同理可得![]() =
=![]() ,
,![]() =1+
=1+![]() =1+
=1+![]() ,
,
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(基础训练)
(1)![]() = ,
= ,![]() = ;
= ;
(2)将![]() 化为分数形式,写出推导过程;
化为分数形式,写出推导过程;
(能力提升)
(3)![]() = ,
= ,![]() = ;
= ;
(注:![]() =0.315315…,
=0.315315…,![]() =2.01818…)
=2.01818…)
(探索发现)
(4)①试比较![]() 与1的大小:
与1的大小:![]() 1(填“>”、“<”或“=”)
1(填“>”、“<”或“=”)
②若已知![]() =
=![]() ,则
,则![]() = .
= .
(注:![]() =0.285714285714…)
=0.285714285714…)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )
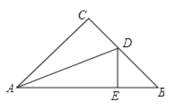
A. 4cm B. 6cm C. 8cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:
若|x1﹣x2|≥|y1﹣y2|,则点P1与点P2的“非常距离”为|x1﹣x2|;
若|x1﹣x2|<|y1﹣y2|,则点P1与点P2的“非常距离”为|y1﹣y2|.
例如:点P1(1,1),点P2(2,3),因为|1﹣2|<|1﹣3|,所以点P1与点P2的“非常距离”为|1﹣3|=2,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q的交点).
(1)已知点A(-![]() ,0),B为y轴上的一个动点.
,0),B为y轴上的一个动点.
①若点B(0,3),则点A与点B的“非常距离”为______;
②若点A与点B的“非常距离”为2,则点B的坐标为_______;
③直接写出点A与点B的“非常距离”的最小值为_______;
(2)已知点D(0,1),点C是直线y=﹣![]() x+3上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.
x+3上的一个动点,如图2,求点C与点D“非常距离”的最小值及相应的点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.
(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以1.5cm/s的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过_____秒后,点P与点Q第一次在△ABC的AC边上相遇?(在横线上直接写出答案,不必书写解题过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com