
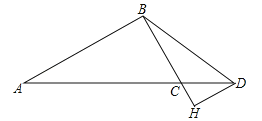
【题目】如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.
(1)求BDcos∠HBD的值;
(2)若∠CBD=∠A,求AB的长.
【答案】(1)4;(2)6.
【解析】
试题分析:(1)首先根据DH∥AB,判断出△ABC∽△DHC,即可判断出![]() =3;然后求出BH的值是多少,再根据在Rt△BHD中,cos∠HBD=
=3;然后求出BH的值是多少,再根据在Rt△BHD中,cos∠HBD=![]() ,求出BDcos∠HBD的值是多少即可;
,求出BDcos∠HBD的值是多少即可;
(2)首先判断出△ABC∽△BHD,推得![]() ;然后根据△ABC∽△DHC,推得
;然后根据△ABC∽△DHC,推得![]() ,所以AB=3DH;最后根据
,所以AB=3DH;最后根据![]() ,求出DH的值是多少,进而求出AB的值是多少即可.
,求出DH的值是多少,进而求出AB的值是多少即可.
试题解析:(1)∵DH∥AB,∴∠BHD=∠ABC=90°,∴△ABC∽△DHC,∴![]() =3,∴CH=1,BH=BC+CH,在Rt△BHD中,cos∠HBD=
=3,∴CH=1,BH=BC+CH,在Rt△BHD中,cos∠HBD=![]() ,∴BDcos∠HBD=BH=4;
,∴BDcos∠HBD=BH=4;
(2)∵∠CBD=∠A,∠ABC=∠BHD,∴△ABC∽△BHD,∴![]() ,∵△ABC∽△DHC,∴
,∵△ABC∽△DHC,∴![]() ,∴AB=3DH,∴
,∴AB=3DH,∴![]() ,解得DH=2,∴AB=3DH=3×2=6,即AB的长是6.
,解得DH=2,∴AB=3DH=3×2=6,即AB的长是6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图是一个等边三角形木框,甲虫P在边框AC上爬行(A,C端点除外),设甲虫P到另外两边的距离之和为d,等边三角形ABC的高为h,则d与h的大小关系是( ) 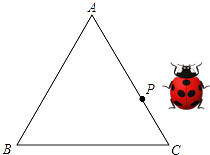
A.d>h
B.d<h
C.d=h
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
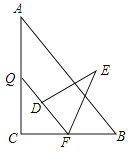
【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长;
(3)若△PDE与△ABC重叠部分图形的周长为T,且12≤T≤16,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某花卉种植基地欲购进甲、乙两种君子兰进行培育,若购进甲种2株,乙种3株,则共需要成本1700元;若购进甲种3株,乙种1株,则共需要成本1500元.
(1)求甲乙两种君子兰每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下购进甲、乙两种君子兰,若购进乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC,AC=BC,∠ACB=90°,AD为角平分线,延长AD交BF于E,E为BF中点,下列结论错误的是( ) 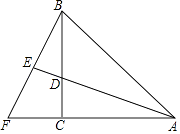
A.AD=BF
B.CF=CD
C.AC+CD=AB
D.BE=CF
查看答案和解析>>
科目:初中数学 来源: 题型:
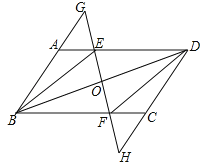
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点0.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什幺特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E,CE=1,延长CE、BA交于点F. 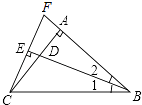
(1)求证:△ADB≌△AFC;
(2)求BD的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com