
如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是 .


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
我们把函数A的图象与直线y=x的公共点叫做函数A的不动点,如二次函数 有两个不动点(0,0)和(10,10).直线y=m是平行于x轴的直线,将抛物线
有两个不动点(0,0)和(10,10).直线y=m是平行于x轴的直线,将抛物线 在直线y=m下侧的部分沿直线y=m翻折,翻折后的部分与没有翻折的部分组成的新的函数B的图象.若函数B刚好有3个不动点,则满足条件的m的值为__________
在直线y=m下侧的部分沿直线y=m翻折,翻折后的部分与没有翻折的部分组成的新的函数B的图象.若函数B刚好有3个不动点,则满足条件的m的值为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
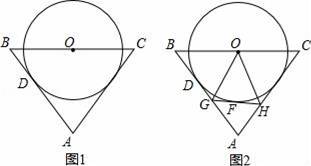
如图1,△ABC中,AB=AC,点O是BC的中点,以O为圆心的⊙O与AB边相切于点D.
(1)判断AC边与⊙O的位置关系,说明理由;
(2)如图2,若AB=5,BC=6,点F为⊙O上一动点,过点F作⊙O的切线分别交AD边、AC边于点G、H,连结OG、OH.
①设∠BAC=α,则∠GOH= (用含α的代数式表示);
②若△OGH是以GH为腰的等腰三角形,求BG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com