
【题目】如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=![]() 的图象经过点Q,若S△BPQ=
的图象经过点Q,若S△BPQ=![]() S△OQC,则k的值为___.
S△OQC,则k的值为___.
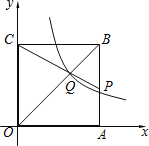
【答案】16
【解析】
根据正方形的性质可得出OC∥AB,从而得出△BPQ∽△OCQ,再根据S△BPQ=![]() S△OCQ,即可得出点P的坐标,利用待定系数法求出直线OB、CP的解析式,联立两个解析式求出交点坐标后再由反比例函数图象上点的坐标特征即可得出结论.
S△OCQ,即可得出点P的坐标,利用待定系数法求出直线OB、CP的解析式,联立两个解析式求出交点坐标后再由反比例函数图象上点的坐标特征即可得出结论.
∵四边形OABC为正方形,
∴OC∥AB,
∴△BPQ∽△OCQ,
∵S△BPQ=![]() S△OCQ,
S△OCQ,
∴BP=![]() AB.
AB.
∵正方形OABC的边长为6,
∴点C(0,6),B(6,6),P(6,3),
利用待定系数法可求出:
直线OB的解析式为y=x,直线CP的解析式为![]()
联立OB、CP的解析式得: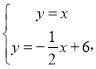
解得:![]()
∴Q(4,4).
∵函数y=![]() 的图象经过点Q,
的图象经过点Q,
∴k=4×4=16.
故答案为:16.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】某小区为“创建文明城市,构建和谐社会”.更好的提高业主垃圾分类的意识,业主委员会决定在小区内安装垃圾分类的温馨提示牌和垃圾箱.若购买3个温馨提示牌和4个垃圾箱共需580元,且每个温馨提示牌比垃圾箱便宜40元.
(1)问:购买1个温馨提示牌和1个垃圾箱各需多少元?
(2)如果需要购买温馨提示牌和垃圾箱共10个,费用不超过800元,问:最多购买垃圾箱多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
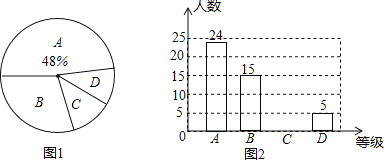
【题目】某销售公司年终进行业绩考核,人事部门把考核结果按照A,B,C,D四个等级,绘制成两个不完整的统计图,如图1,图2.
![]() 参加考试的人数是______,扇形统计图中D部分所对应的圆心角的度数是______,请把条形统计图补充完整;
参加考试的人数是______,扇形统计图中D部分所对应的圆心角的度数是______,请把条形统计图补充完整;
![]() 若公司领导计划从考核人员中选一人交流考核意见,求所选人员考核为A等级的概率;
若公司领导计划从考核人员中选一人交流考核意见,求所选人员考核为A等级的概率;
![]() 为推动公司进一步发展,公司决定计划两年内考核A等级的人数达到30人,求平均每年的增长率
为推动公司进一步发展,公司决定计划两年内考核A等级的人数达到30人,求平均每年的增长率![]() 精确到
精确到![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
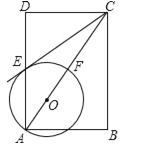
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
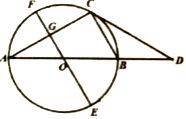
【题目】如图,⊙O是△ABC的外接圆,AB为⊙O的直径,过点C作∠BCD=∠CAB交AB的延长线于点D,过点O作直径EF∥BC,交AC于点G.
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为2,∠BCD=30°.
①连接AE、DE,求证:四边形ACDE是菱形.
②当点P是线段AD上的一动点时,求PF+PG的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
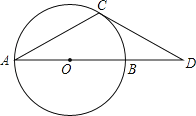
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,点C在⊙O上,CA=CD,∠CDA=30°.
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,
①用尺规作出点A到CD所在直线的距离;
②求出该距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
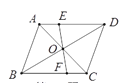
【题目】如图,平行四边形ABCD的周长是18 cm,其对角线AC,BD相交于点O,过点O的直线分别与AD,BC相交于点E,F,且OE=2 cm,则四边形CDEF的周长是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
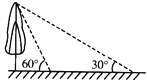
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com