
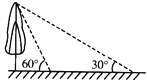
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
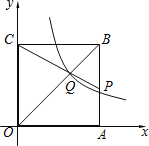
【题目】如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=![]() 的图象经过点Q,若S△BPQ=
的图象经过点Q,若S△BPQ=![]() S△OQC,则k的值为___.
S△OQC,则k的值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求二次函数的解析式;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;
(3)若直线与y轴的交点为E,连结AD、AE,求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
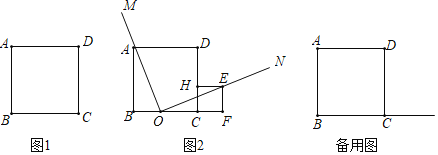
【题目】正方形ABCD的边长为1,点O是BC边上的一个动点(与B,C不重合),以O为顶点在BC所在直线的上方作∠MON=90°
(1)当OM经过点A时,
①请直接填空:ON______(可能,不可能)过D点:(图1仅供分析)
②如图2,在ON上截取OE=OA,过E点作EF垂直于直线BC,垂足为点F,作EH⊥CD于H,求证:四边形EFCH为正方形;
③如图2,将②中的已知与结论互换,即在ON上取点E(E点在正方形ABCD外部),过E点作EF垂直于直线BC,垂足为点F,作EH⊥CD于H,若四边形EFCH为正方形,那么OE与OA是否相等?请说明理由;
(2)当点O在射线BC上且OM不过点A时,设OM交边AB于G,且OG=2.在ON上存在点P,过P点作PK垂直于直线BC,垂足为点K,使得S△PKO=![]() S△OBG,连接GP,则当BO为何值时,四边形PKBG的面积最大?最大面积为多少?
S△OBG,连接GP,则当BO为何值时,四边形PKBG的面积最大?最大面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
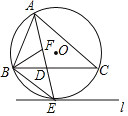
【题目】如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点E,且l∥BC.
(1)求证:AE平分∠BAC;
(2)作∠ABC的平分线BF交AE于点F,求证:BE=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
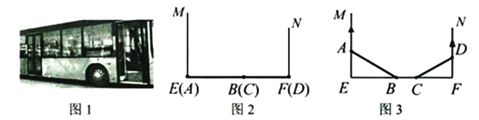
【题目】图2、图3是某公共汽车双开门的俯视示意图,ME,EF,FN是门轴的滑动轨道,![]() ,两门AB,CD的门轴A,B,C,D都在滑动轨道上,两门关闭时图2,A,D分别在E,F处,门缝忽略不计(即B,C重合);两门同时开启,A,D分别沿
,两门AB,CD的门轴A,B,C,D都在滑动轨道上,两门关闭时图2,A,D分别在E,F处,门缝忽略不计(即B,C重合);两门同时开启,A,D分别沿![]() ,
,![]() 的方向匀速滑动,带动B,C滑动;B到达E时,C恰好到达F,此时两门完全开启.已知
的方向匀速滑动,带动B,C滑动;B到达E时,C恰好到达F,此时两门完全开启.已知![]() .(1)如图3,当
.(1)如图3,当![]() 时,
时,![]() ______cm.(2)在(1)的基础上,当A向M方向继续滑动15cm时,四边形ABCD的面积为______
______cm.(2)在(1)的基础上,当A向M方向继续滑动15cm时,四边形ABCD的面积为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(m﹣3)x﹣m(2m﹣3)=0
(1)证明:无论m为何值方程都有两个实数根;
(2)是否存在正数m,使方程的两个实数根的平方和等于26?若存在,求出满足条件的正数m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做“用频率估计概率”的试验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 任意买一张电影票,座位号是2的倍数的概率
B. 一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃
C. 抛一个质地均匀的正方体骰子,落下后朝上的面点数是3
D. 一个不透明的袋子中有4个白球、1个黑球,它们除了颜色外都相同,从中抽到黑球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com