
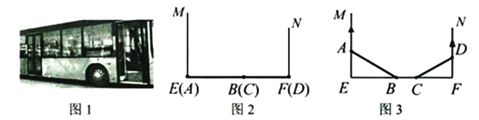
����Ŀ��ͼ2��ͼ3��ij��������˫���ŵĸ���ʾ��ͼ��ME,EF,FN������Ļ��������![]() ,����AB,CD������A,B,C,D���ڻ�������ϣ����Źر�ʱͼ2��A,D�ֱ���E,F�����ŷ���Բ��ƣ���B,C�غϣ�������ͬʱ������A,D�ֱ���
,����AB,CD������A,B,C,D���ڻ�������ϣ����Źر�ʱͼ2��A,D�ֱ���E,F�����ŷ���Բ��ƣ���B,C�غϣ�������ͬʱ������A,D�ֱ���![]() ,
,![]() �ķ������ٻ���������B,C������B����Eʱ��Cǡ�õ���F����ʱ������ȫ��������֪
�ķ������ٻ���������B,C������B����Eʱ��Cǡ�õ���F����ʱ������ȫ��������֪![]() ����1����ͼ3����
����1����ͼ3����![]() ʱ��
ʱ��![]() ______cm����2���ڣ�1���Ļ����ϣ���A��M�����������15cmʱ���ı���ABCD�����Ϊ______
______cm����2���ڣ�1���Ļ����ϣ���A��M�����������15cmʱ���ı���ABCD�����Ϊ______![]() ��
��
���𰸡���1��![]() �� ��2��2256��
�� ��2��2256��
��������
��1������֪�ɵ�B��C�����·��֮��Ϊ5��4���ٽ��B�˶���·�̼������C�˶���·�̣���Ӽ������BC�ij�����2����A��M�����������15cmʱ��AA'��15cm���ɹ��ɶ�������Ŀ���������A'EB'����D'FC'������A'EFD'�߳����������ø������ı����ı���ABCD�������
��A��D�ֱ���E��F�����ŷ���Բ��ƣ���B��C�غϣ���AB��50cm��CD��40cm��
��EF��50+40��90cm
��B����Eʱ��Cǡ�õ���F����ʱ������ȫ������
��B��C�����·��֮��Ϊ5��4
��1������ABE��30��ʱ����Rt��ABE�У�![]() ��
��
��B�˶���·��Ϊ��50��25![]() ��cm
��cm
��B��C�����·��֮��Ϊ5��4
���ʱ��C�˶���·��Ϊ![]() cm
cm
��BC����50��25![]() ��+��40��20
��+��40��20![]() ������90��45
������90��45![]() ��cm
��cm
�ʴ�Ϊ��90��45![]() ��
��
��2����A��M�����������15cmʱ�����ʱ��A�˶����˵�A'������B��C��D�ֱ��˶����˵�B'��C'��D'��������A'D'����ͼ��
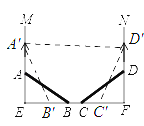
���ʱAA'��15cm
��A'E��15+25��40cm
�ɹ��ɶ����ã�EB'��30cm��
��B�˶���·��Ϊ50��30��20cm
��C�˶���·��Ϊ16cm
��C'F��40��16��24cm
�ɹ��ɶ����ã�D'F��32cm��
���ı���A'B'C'D'�����������A'EFD'���������A'EB'���������D'FC'�������![]() ��24��32��2556cm2��
��24��32��2556cm2��
���ı���ABCD�����Ϊ2556cm2��
�ʴ�Ϊ��2556��


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
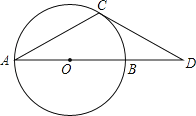
����Ŀ����ͼ��AB����O��ֱ������D��AB���ӳ����ϣ���C����O�ϣ�CA��CD����CDA��30�㣮
��1�����ж�ֱ��CD����O��λ�ù�ϵ����˵�����ɣ�
��2������O�İ뾶Ϊ4��
���ó߹�������A��CD����ֱ�ߵľ��룻
������þ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
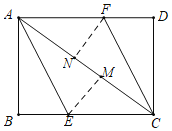
����Ŀ����ͼ��ACΪ����ABCD�ĶԽ��ߣ�����AB��AE�۵���ʹ��B����AC�ϵĵ�M��������CD��CF�۵���ʹ��D����AC�ϵĵ�N����
��1����֤���ı���AECF��ƽ���ı��Σ�
��2������BAEΪ���ٶ�ʱ���ı���AECF�����Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
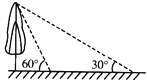
����Ŀ����ͼ��У����һ������洹ֱ��������ѧ��ȤС�����β������ڵ����ϵ�Ӱ�ӣ���һ��������������60����ʱ���ڶ���������������30����ʱ�����β�����Ӱ�����8�ף�������_____________��(�����������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
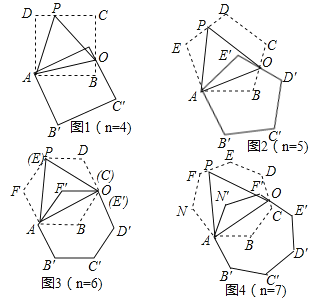
����Ŀ����ͼ������n�����Ƶ�A˳ʱ����ת60��������תǰ����ͼ������һ����O������AO�����dz�AOΪ�����������ٽ���������AO���ڵ�ֱ���Ƶ�A��ʱ����ת60������תǰ��ͼ���ڵ�P������PO�����dz���OABΪ�����ҽ�������AOPΪ����������������
��̽��֤����
��1������ͼ1��ͼ2��ѡ������һ��֤����������������������AOP���ǵȱ������Σ�
��2����ͼ2����֤����OAB=��OAE����
�����ɲ��룩
��3��ͼ1��ͼ2�е������ҽ����Ķ����ֱ�Ϊ �� ��
��4��ͼn�У��������������� �ȱ������Σ���������������������
��5��ͼn�У������ҽ����Ķ���Ϊ ���ú�n��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���![]() �У�
�У�![]() ����D,E�ֱ��ڱ�AB,BC�ϣ����߶�ED�Ƶ�E����ʱ�뷽����ת90�õ�EF��
����D,E�ֱ��ڱ�AB,BC�ϣ����߶�ED�Ƶ�E����ʱ�뷽����ת90�õ�EF��

��1����ͼ1����![]() ����E���C�غϣ�AF��DC�ཻ�ڵ�O����֤��
����E���C�غϣ�AF��DC�ཻ�ڵ�O����֤��![]() ��
��
��2����֪��GΪAF���е㣮
����ͼ2����![]() ����DG�ij���
����DG�ij���
����![]() ���Ƿ���ڵ�E��ʹ��
���Ƿ���ڵ�E��ʹ��![]() ��ֱ�������Σ������ڣ���CE�ij����������ڣ���˵�����ɣ�
��ֱ�������Σ������ڣ���CE�ij����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮ��ɽ���ǽ�ɽ��ɽ������������ˮƽ����ߣ����Ƕ���ˮƷ�ʵ�����Խ��Խ��.Т���л���˾�����г��������![]() ��
��![]() �����ͺŵľ�ˮ����ÿ̨
�����ͺŵľ�ˮ����ÿ̨![]() �;�ˮ����ÿ̨
�;�ˮ����ÿ̨![]() �;�ˮ�����۶�200Ԫ����5��Ԫ����
�;�ˮ�����۶�200Ԫ����5��Ԫ����![]() �;�ˮ������4.5��Ԫ����
�;�ˮ������4.5��Ԫ����![]() �;�ˮ�����������.
�;�ˮ�����������.
��1����ÿ̨![]() �͡�
�͡�![]() �;�ˮ���Ľ��۸��Ƕ���Ԫ��
�;�ˮ���Ľ��۸��Ƕ���Ԫ��
��2������˾�ƻ�����![]() ��
��![]() �����ͺŵľ�ˮ����50̨��������������
�����ͺŵľ�ˮ����50̨��������������![]() �;�ˮ��Ϊ
�;�ˮ��Ϊ![]() ̨�������ʽ���9.8��Ԫ.����ʱ
̨�������ʽ���9.8��Ԫ.����ʱ![]() �;�ˮ��ÿ̨�ۼ�2500Ԫ��
�;�ˮ��ÿ̨�ۼ�2500Ԫ��![]() �;�ˮ��ÿ̨�ۼ�2180Ԫ.����˾����������
�;�ˮ��ÿ̨�ۼ�2180Ԫ.����˾����������![]() �;�ˮ���������а�ÿ̨����
�;�ˮ���������а�ÿ̨����![]() Ԫ��Ϊ��˾���ƶ������ˮ�����ʽ��軱��˾����50̨��ˮ��������ƶ�ʽ���õ�����Ϊ
Ԫ��Ϊ��˾���ƶ������ˮ�����ʽ��軱��˾����50̨��ˮ��������ƶ�ʽ���õ�����Ϊ![]() ����
����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ÿ��С�����εı߳�Ϊ1������ͼ���У�ÿ��С�����εĶ����Ϊ���.��ͼ��5��5�����η���ֽͼ�У���A��B���ڸ�㴦.
(1)����ͼ����������ABC��ʹ��ױ�AC��2![]() ���ҵ�CΪ��㣻
���ҵ�CΪ��㣻
(2)��(1)�������£�����ƽ���ı���ABDC����DΪ��㣬��ֱ��д��ƽ���ı���ABDC�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ��5�µĵڶ��������ռ�Ϊĸ�ڣ�����ĸ�����أ�������Ъʱ������������ϲ����ĸ��Ϊĸ�����ʻ����ж�ĸ�ף�ף��ĸ��. ����ǰϦ��ij����ɹ���һ���ʻ���У��ɱ���Ϊ30Ԫÿ����������һ��ĸ�ڵ��ʻ��������������õ����������ݣ�ͬʱ����ÿ���������![]() �����������۵���
�����������۵���![]() ��Ԫ/������һ�κ���.
��Ԫ/������һ�κ���.
���۵��� | �� | 30 | 40 | 50 | 60 | �� |
ÿ�������� | �� | 350 | 300 | 250 | 200 | �� |
��1�����![]() ��
��![]() �ĺ�����ϵ��
�ĺ�����ϵ��
��2����۾�Ҫ��,���۸��ʻ���л�õ����ø���100����
�������۵���![]() ȡ��ֵʱ,�û��������ʻ����ÿ���õ�����Ϊ5000Ԫ?(����=�����ܼ�-�ɱ���)��
ȡ��ֵʱ,�û��������ʻ����ÿ���õ�����Ϊ5000Ԫ?(����=�����ܼ�-�ɱ���)��
����ȷ�����۵���![]() ȡ��ֵʱ�����������ʻ����ÿ���õ�����
ȡ��ֵʱ�����������ʻ����ÿ���õ�����![]() ��Ԫ�����������������ʻ����ÿ���õ��������.
��Ԫ�����������������ʻ����ÿ���õ��������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com