
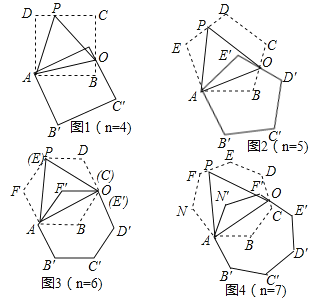
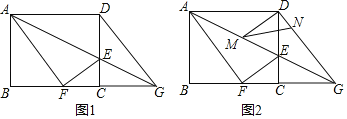
【题目】如图,将正n边形绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为“叠弦角”,△AOP为“叠弦三角形”.
(探究证明)
(1)请在图1和图2中选择其中一个证明:“叠弦三角形”(△AOP)是等边三角形;
(2)如图2,求证:∠OAB=∠OAE′.
(归纳猜想)
(3)图1、图2中的“叠弦角”的度数分别为 , ;
(4)图n中,“叠弦三角形” 等边三角形(填“是”或“不是”)
(5)图n中,“叠弦角”的度数为 (用含n的式子表示)
【答案】(1)证明见解析;(2)证明见解析;(3)15°,24°;(4)是;(5)![]() .
.
【解析】
(1)先由旋转的性质,再判断出△APD≌△AOD/,最后用旋转角计算即可;
(2)向判断出Rt△AEM≌△Rt△ABN,在判断出Rt△APM≌Rt△AON即可;
(3)先判断出△AD/O≌△ABO,再利用正方形,正五边形的性质和旋转的性质,计算即可;
(4)先判断出△APF≌△AE/F/,再用旋转角60°,从而得出△PAO是等边三角形;
(5)用(3)的方法求出正n边形的“叠弦角”的度数.
解:(1)如图1,
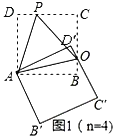
∵四边形ABCD是正方形, 由旋转知:AD=AD',∠D=∠D'=90°,∠DAD'=∠OAP=60°,
∴∠DAP=∠D'AO,∴△APD≌△AOD'(ASA)∴AP=AO,
∵∠OAP=60°,∴△AOP是等边三角形,
(2)如图2,作AM⊥DE于M,作AN⊥CB于N.
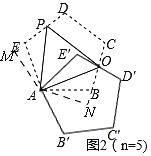
∵五边形ABCDE是正五边形,
由旋转知:AE=AE',∠E=∠E'=108°,∠EAE'=∠OAP=60°
∴∠EAP=∠E'AO ∴△APE≌△AOE'(ASA)
∴∠OAE'=∠PAE.
在Rt△AEM和Rt△ABN中,∠AEM=∠ABN=72°,AE=AB
∴Rt△AEM≌Rt△ABN (AAS), ∴∠EAM=∠BAN,AM=AN.
在Rt△APM和Rt△AON中,AP=AO,AM=AN
∴Rt△APM≌Rt△AON (HL).∴∠PAM=∠OAN,
∴∠PAE=∠OAB ∴∠OAE'=∠OAB (等量代换).
(3)由(1)有,△APD≌△AOD',
∴∠DAP=∠D′AO,
在△AD′O和△ABO中,
AD′=AB,AO=AO,
∴△AD′O≌△ABO,∴∠D′AO=∠BAO,
由旋转得,∠DAD′=60°,∵∠DAB=90°,∴∠D′AB=∠DAB﹣∠DAD′=30°,
∴∠D′AD=![]() ∠D′AB=15°,
∠D′AB=15°,
同理可得,∠E′AO=24°,
故答案为:15°,24°.
(4)如图3,
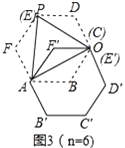
∵六边形ABCDEF和六边形A′B′C′E′F′是正六边形,∴∠F=F′=120°,由旋转得,AF=AF′,EF=E′F′,∴△APF≌△AE′F′,∴∠PAF=∠E′AF′,
由旋转得,∠FAF′=60°,AP=AO ∴∠PAO=∠FAO=60°,
∴△PAO是等边三角形.故答案为:是
(5)图n中的多边形是正(n+3)边形,
同(3)的方法得,![]()
故答案:![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知A,B,C,D四点的坐标依次为(0,0),(6,2),(8,8),(2,6),若一次函数y=mx﹣6m+2(m≠0)图象将四边形ABCD的面积分成1:3两部分,则m的值为( )
A. ﹣4B. ![]() ,﹣5C.
,﹣5C. ![]() D.
D. ![]() ,﹣4
,﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠,顶点
折叠,顶点![]() 恰好落在
恰好落在![]() 边上点
边上点![]() 处,延长
处,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求线段![]() 的长;
的长;
(2)如图2,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上的动点(与端点不重合),且
上的动点(与端点不重合),且![]() ,设
,设![]() ,
,![]() .
.
①写出![]() 关于
关于![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的最小值;
的最小值;
②是否存在这样的点![]() ,使
,使![]() 是等腰三角形?若存在,请求出
是等腰三角形?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
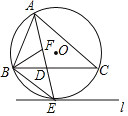
【题目】如图,⊙O是△ABC的外接圆,直线l与⊙O相切于点E,且l∥BC.
(1)求证:AE平分∠BAC;
(2)作∠ABC的平分线BF交AE于点F,求证:BE=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图.

根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生,其中安全意识为“很强”的学生占被调查学生总数的百分比是 ;
(2)请将条形统计图补充完整;
(3)该校有1800名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有 名.
查看答案和解析>>
科目:初中数学 来源: 题型:
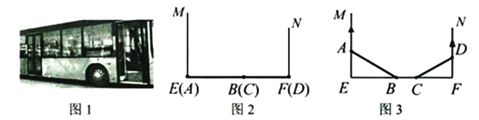
【题目】图2、图3是某公共汽车双开门的俯视示意图,ME,EF,FN是门轴的滑动轨道,![]() ,两门AB,CD的门轴A,B,C,D都在滑动轨道上,两门关闭时图2,A,D分别在E,F处,门缝忽略不计(即B,C重合);两门同时开启,A,D分别沿
,两门AB,CD的门轴A,B,C,D都在滑动轨道上,两门关闭时图2,A,D分别在E,F处,门缝忽略不计(即B,C重合);两门同时开启,A,D分别沿![]() ,
,![]() 的方向匀速滑动,带动B,C滑动;B到达E时,C恰好到达F,此时两门完全开启.已知
的方向匀速滑动,带动B,C滑动;B到达E时,C恰好到达F,此时两门完全开启.已知![]() .(1)如图3,当
.(1)如图3,当![]() 时,
时,![]() ______cm.(2)在(1)的基础上,当A向M方向继续滑动15cm时,四边形ABCD的面积为______
______cm.(2)在(1)的基础上,当A向M方向继续滑动15cm时,四边形ABCD的面积为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
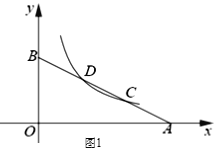
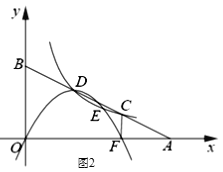
【题目】如图,已知A,B两点分别在x轴和y轴的正半轴上,连接AB与反比例函数![]() 的图象交于C、D两点.
的图象交于C、D两点.
(1)当0A=6,OB=3,点D的横坐标为2时,则k=____,![]() =_______.
=_______.
(2)当0A=a,OB=b时,请猜测AC与BD之间的数量关系,并说明理由.
(3)如图,以D为顶点且过点O的抛物线分别交函数![]() 的图像和x轴于点E、F,连接CF,设
的图像和x轴于点E、F,连接CF,设![]() =m..
=m..
①若∠AFC=90°,则m的值为多少?
②若∠ACF=90°,且m>![]() 时,请用含m的代数式表示tan∠BAO的值.
时,请用含m的代数式表示tan∠BAO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商设计了一款制造成本为18元新型电子厂品,投放市场进行试销.经过调查,得到每月销售量y(万件)与销售单价x(元)之间的部分数据如下:
销售单价x(元/件) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 30 | … |
(1)求出每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)求出每月的利润z(万元)与销售单x(元)之间的函数关系式.
(3)根据相关部门规定,这种电子产品的销售利润率不能高于50%,而且该电子厂制造出这种产品每月的制造成本不能超过900万元.那么并求出当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?(利润=售价﹣制造成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com