
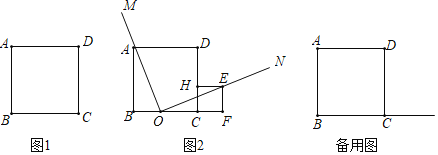
【题目】正方形ABCD的边长为1,点O是BC边上的一个动点(与B,C不重合),以O为顶点在BC所在直线的上方作∠MON=90°
(1)当OM经过点A时,
①请直接填空:ON______(可能,不可能)过D点:(图1仅供分析)
②如图2,在ON上截取OE=OA,过E点作EF垂直于直线BC,垂足为点F,作EH⊥CD于H,求证:四边形EFCH为正方形;
③如图2,将②中的已知与结论互换,即在ON上取点E(E点在正方形ABCD外部),过E点作EF垂直于直线BC,垂足为点F,作EH⊥CD于H,若四边形EFCH为正方形,那么OE与OA是否相等?请说明理由;
(2)当点O在射线BC上且OM不过点A时,设OM交边AB于G,且OG=2.在ON上存在点P,过P点作PK垂直于直线BC,垂足为点K,使得S△PKO=![]() S△OBG,连接GP,则当BO为何值时,四边形PKBG的面积最大?最大面积为多少?
S△OBG,连接GP,则当BO为何值时,四边形PKBG的面积最大?最大面积为多少?
【答案】(1)①不可能②见解析③OA=OE(2)当BO为![]() 时,四边形PKBG的面积最大,最大面积为
时,四边形PKBG的面积最大,最大面积为![]()
【解析】
(1)①若ON过点D时,则在△OAD中不满足勾股定理,可知不可能过D点;
②由条件可先判业四边形EFCH为矩形,再证明△OFE≌△ABO,可证得结论;
③结论:OA=OE.如图2-1中,连接EC,在BA上取一点Q,使得BQ=BO,连接OQ.证明△AQO≌△OCE(ASA)即可.
(2)由条件可证明△PKO∽△OBG,利用相似三角形的性质可求得OP=2,可求得△POG面积为定值及△PKO和△OBG的关系,只要△CGB的面积有最大值时,则四边形PKBG的面积就最大,设OB=a,BG=b,由勾股定理可用b表示出a,则可用a表示出△OBG的面积,利用二次函数的性质可求得其最大值,则可求得四边形PKBG面积的最大值.
(1)①若ON过点D,则OA>AB,OD>CD,
∴OA2>AD2,OD2>AD2,
∴OA2+OD2>2AD2≠AD2,
∴∠AOD≠90°,这与∠MON=90°矛盾,
∴ON不可能过D点,
故答案为:不可能;
②如图2中,∵EH⊥CD,EF⊥BC,
∴∠EHC=∠EFC=90°,且∠HCF=90°,
∴四边形EFCH为矩形,
∵∠MON=90°,
∴∠EOF=90°-∠AOB,
在正方形ABCD中,∠BAO=90°-∠AOB,
∴∠EOF=∠BAO,
在△OFE和△ABO中,
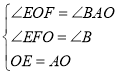
∴△OFE≌△ABO(AAS),
∴EF=OB,OF=AB,
又OF=CF+OC=AB=BC=BO+OC=EF+OC,
∴CF=EF,
∴四边形EFCH为正方形;
③结论:OA=OE.
理由:如图2-1中,连接EC,在BA上取一点Q,使得BQ=BO,连接OQ.
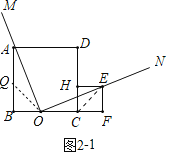
∵AB=BC,BQ=BO,
∴AQ=QC,
∵∠QAO=∠EOC,∠AQO=∠ECO=135°,
∴△AQO≌△OCE(ASA),
∴AO=OE.
(2)
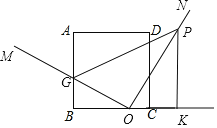
∵∠POK=∠OGB,∠PKO=∠OBG,
∴△PKO∽△OBG,
∵S△PKO=![]() S△OBG,
S△OBG,
∴
∴OP=1,
∴S△POG=![]() OGOP=
OGOP=![]() ×1×2=1,
×1×2=1,
设OB=a,BG=b,则a2+b2=OG2=4,
∴b=![]()
∴![]()
∴当a2=2时,△OBG有最大值1,此时S△PKO=![]() S△OBG=
S△OBG=![]() ,
,
∴四边形PKBG的最大面积为1+1+![]() =
=![]() .
.
∴当BO为![]() 时,四边形PKBG的面积最大,最大面积为
时,四边形PKBG的面积最大,最大面积为![]() .
.


科目:初中数学 来源: 题型:
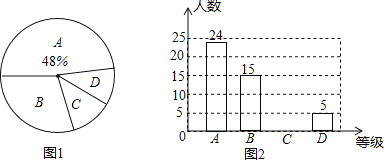
【题目】某销售公司年终进行业绩考核,人事部门把考核结果按照A,B,C,D四个等级,绘制成两个不完整的统计图,如图1,图2.
![]() 参加考试的人数是______,扇形统计图中D部分所对应的圆心角的度数是______,请把条形统计图补充完整;
参加考试的人数是______,扇形统计图中D部分所对应的圆心角的度数是______,请把条形统计图补充完整;
![]() 若公司领导计划从考核人员中选一人交流考核意见,求所选人员考核为A等级的概率;
若公司领导计划从考核人员中选一人交流考核意见,求所选人员考核为A等级的概率;
![]() 为推动公司进一步发展,公司决定计划两年内考核A等级的人数达到30人,求平均每年的增长率
为推动公司进一步发展,公司决定计划两年内考核A等级的人数达到30人,求平均每年的增长率![]() 精确到
精确到![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
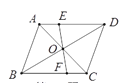
【题目】如图,平行四边形ABCD的周长是18 cm,其对角线AC,BD相交于点O,过点O的直线分别与AD,BC相交于点E,F,且OE=2 cm,则四边形CDEF的周长是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离![]() 与小王的行驶时间
与小王的行驶时间![]() 之间的函数关系.
之间的函数关系.
请你根据图象进行探究:
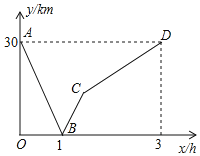
(1)小王和小李的速度分别是多少?
(2)求线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
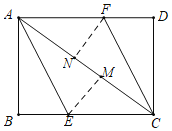
【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是平行四边形;
(2)当∠BAE为多少度时,四边形AECF是菱形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
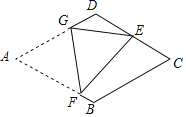
【题目】如图,在菱形纸片ABCD中,AB=4,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则sin∠EFG的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
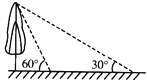
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() .点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90得到EF.
.点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90得到EF.

(1)如图1,若![]() ,点E与点C重合,AF与DC相交于点O.求证:
,点E与点C重合,AF与DC相交于点O.求证:![]() .
.
(2)已知点G为AF的中点.
①如图2,若![]() ,求DG的长.
,求DG的长.
②若![]() ,是否存在点E,使得
,是否存在点E,使得![]() 是直角三角形?若存在,求CE的长;若不存在,试说明理由.
是直角三角形?若存在,求CE的长;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现
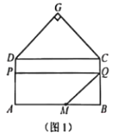
如图,四边形ABCD是矩形,AB=20,BC=10,以CD为一边向矩形外部作等腰直角△GDC,∠G=90°,点M在线段AB上,且AM=a,点P沿折线AD-DG运动,点Q沿折线BC-CG运动(与点G不重合),在运动过程中始终保持线段PQ//AB.设PQ与AB之间的距离为x.
(1)若a=12.①如图1,当点P在线段AD上时,若四边形AMQP的面积为48,则x的值为_________;
②在运动过程中,求四边形AMQP的最大面积;
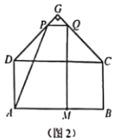
(2)如图2,若点P在线段DG上时,要使四边形AMQP的面积始终不小于50,求a的取值范围.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com