
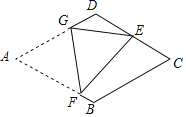
【题目】如图,在菱形纸片ABCD中,AB=4,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则sin∠EFG的值为________.
【答案】![]()
【解析】试题解析:作EH⊥AD于H,连接BE、BD,连接AE交FG于O,如图,
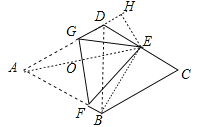
∵四边形ABCD为菱形,∠A=60°,∴△BDC为等边三角形,∠ADC=120°,∵E点为CD的中点,∴CE=DE=1,BE⊥CD,在Rt△BCE中,BE=![]() CE=
CE=![]() ,∵AB∥CD,∴BE⊥AB,设AF=x,∵菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,∴EF=AF,FG垂直平分AE,∠EFG=∠AFG,在Rt△BEF中,(2﹣x)2+(
,∵AB∥CD,∴BE⊥AB,设AF=x,∵菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,∴EF=AF,FG垂直平分AE,∠EFG=∠AFG,在Rt△BEF中,(2﹣x)2+(![]() )2=x2,解得x=
)2=x2,解得x=![]() ,在Rt△DEH中,DH=
,在Rt△DEH中,DH=![]() DE=
DE=![]() ,HE=
,HE=![]() DH=
DH=![]() ,在Rt△AEH中,AE=
,在Rt△AEH中,AE=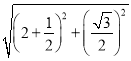 =
=![]() ,∴AO=
,∴AO=![]() ,在Rt△AOF中,OF=
,在Rt△AOF中,OF=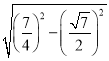 =
=![]() ,∴cos∠AFO=
,∴cos∠AFO=![]() =
=![]() .故答案为:
.故答案为: ![]() .
.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
求证:(1)△ABD≌△GCA;
(2)AD=AG.

查看答案和解析>>
科目:初中数学 来源: 题型:
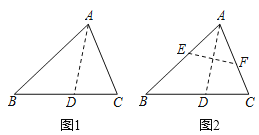
【题目】(1)观察与发现:
小明将三角形纸片![]() (
(![]() )沿过点
)沿过点![]() 的直线折叠,使得
的直线折叠,使得![]() 落在
落在![]() 边上,折痕为
边上,折痕为![]() ,展开纸片(如图1);在第一次的折叠基础上第二次折叠该三角形纸片,使点
,展开纸片(如图1);在第一次的折叠基础上第二次折叠该三角形纸片,使点![]() 和点
和点![]() 重合,折痕为
重合,折痕为![]() ,展平纸片后得到
,展平纸片后得到![]() (如图2).小明认为
(如图2).小明认为![]() 是等腰三角形,你同意他的结论吗?请说明理由:
是等腰三角形,你同意他的结论吗?请说明理由:
(2)模型与运用:
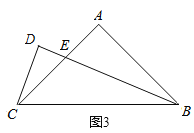
如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
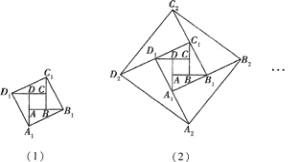
【题目】如图(1),已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2(如图(2));以此下去,则正方形AnBnCnDn的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
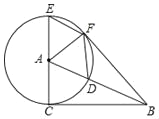
【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF、DF
(1)求证:BF是⊙A的切线.
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com