
【题目】(1)观察与发现:
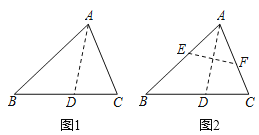
小明将三角形纸片![]() (
(![]() )沿过点
)沿过点![]() 的直线折叠,使得
的直线折叠,使得![]() 落在
落在![]() 边上,折痕为
边上,折痕为![]() ,展开纸片(如图1);在第一次的折叠基础上第二次折叠该三角形纸片,使点
,展开纸片(如图1);在第一次的折叠基础上第二次折叠该三角形纸片,使点![]() 和点
和点![]() 重合,折痕为
重合,折痕为![]() ,展平纸片后得到
,展平纸片后得到![]() (如图2).小明认为
(如图2).小明认为![]() 是等腰三角形,你同意他的结论吗?请说明理由:
是等腰三角形,你同意他的结论吗?请说明理由:
(2)模型与运用:
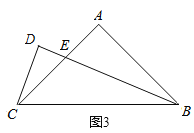
如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,求
,求![]() 的面积.
的面积.
科目:初中数学 来源: 题型:
【题目】如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;

(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:

(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店出售一种水果,经过市场估算,若每个售价为20元时,每周可卖出300个.经过市场调查,如果每个水果每降价1元,每周可多卖出25个,若设每个水果的售价为x元(x<20).
(1)则这一周可卖出这种水果为________个(用含x的代数式表示);
(2)若该周销售这种水果的收入为6400元,那么每个水果的售价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形纸片ABCD中,AB=4,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则sin∠EFG的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)模型建立:
如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() .求证:
.求证:![]() ;
;
(2)模型应用:
①如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,以线段
,以线段![]() 为腰在第一象限内作等腰直角三角形
为腰在第一象限内作等腰直角三角形![]() ,则
,则![]() 点的坐标为___________(直接写出结果)
点的坐标为___________(直接写出结果)
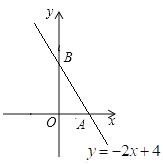
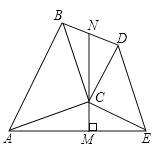
②如图,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 、
、![]() ,作
,作![]() 于
于![]() 点,延长
点,延长![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证:![]() 是
是![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,在边
,在边![]() 上顺次取点
上顺次取点![]() ,
,![]() ,
,![]() …,在边
…,在边![]() 上顺次取点
上顺次取点![]() ,
,![]() ,
,![]() …,使得
…,使得![]() …,得到等腰△
…,得到等腰△![]() ,△
,△![]() ,△
,△![]() ,△
,△![]() …
…

(1)若![]() =30°,可以得到的最后一个等腰三角形是_________;
=30°,可以得到的最后一个等腰三角形是_________;
(2)若按照上述方式操作,得到的最后一个等腰三角形是△![]() ,则
,则![]() 的度数
的度数![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com