
【题目】如图,已知![]() ,在边
,在边![]() 上顺次取点
上顺次取点![]() ,
,![]() ,
,![]() …,在边
…,在边![]() 上顺次取点
上顺次取点![]() ,
,![]() ,
,![]() …,使得
…,使得![]() …,得到等腰△
…,得到等腰△![]() ,△
,△![]() ,△
,△![]() ,△
,△![]() …
…

(1)若![]() =30°,可以得到的最后一个等腰三角形是_________;
=30°,可以得到的最后一个等腰三角形是_________;
(2)若按照上述方式操作,得到的最后一个等腰三角形是△![]() ,则
,则![]() 的度数
的度数![]() 的取值范围是________.
的取值范围是________.
【答案】△![]() ;
; ![]()
【解析】
(1)根据等腰三角形性质得:∠O=∠OP2P1,∠P2P1P3=∠P2P3P1, ∠P3P2P4=∠P3P4P2, ∠P4P3P5=∠P4P5P3,根据三角形内角和性质得∠P3P4P2不可能等于90°;(2)由(1)可得∠MP4P5=5∠O=5![]() ,∠NP5P4=4
,∠NP5P4=4![]() ;∠MP4P5≤90°, ∠NP5P4<90°.
;∠MP4P5≤90°, ∠NP5P4<90°.
(1)因为![]()
所以∠O=∠OP2P1,∠P2P1P3=∠P2P3P1, ∠P3P2P4=∠P3P4P2, ∠P4P3P5=∠P4P5P3,
若![]() =30°
=30°
则∠P2P1P3=∠P2P3P1=∠O+∠OP2P1=60°
所以∠P3P2P4=∠P2P3P1+∠O=60°+30°=90°
因为∠P3P4P2不可能等于90°
所以若![]() =30°,可以得到的最后一个等腰三角形是△
=30°,可以得到的最后一个等腰三角形是△![]() ;
;
(2)由(1)可得∠MP4P5=5∠O=5![]() ,∠NP5P4=4
,∠NP5P4=4![]() ;
;
∠MP4P5≤90°, ∠NP5P4<90°,即5![]() ≤90°, 4
≤90°, 4![]() <90°,
<90°,
所以![]()
所以得到的最后一个等腰三角形是△![]() ,则
,则![]() 的度数
的度数![]() 的取值范围是
的取值范围是![]()
故答案为:△![]() ;
;![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
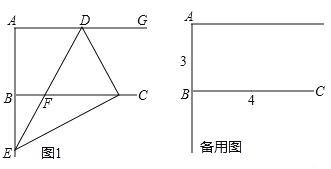
【题目】(1)观察与发现:
小明将三角形纸片![]() (
(![]() )沿过点
)沿过点![]() 的直线折叠,使得
的直线折叠,使得![]() 落在
落在![]() 边上,折痕为
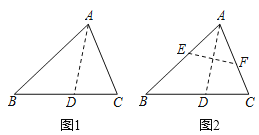
边上,折痕为![]() ,展开纸片(如图1);在第一次的折叠基础上第二次折叠该三角形纸片,使点
,展开纸片(如图1);在第一次的折叠基础上第二次折叠该三角形纸片,使点![]() 和点
和点![]() 重合,折痕为
重合,折痕为![]() ,展平纸片后得到
,展平纸片后得到![]() (如图2).小明认为
(如图2).小明认为![]() 是等腰三角形,你同意他的结论吗?请说明理由:
是等腰三角形,你同意他的结论吗?请说明理由:
(2)模型与运用:
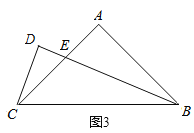
如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
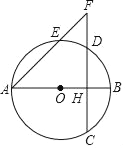
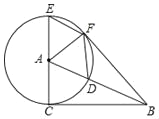
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足H在半径OB上,AH=5,CD=![]() ,点E在弧AD上,射线AE与CD的延长线交于点F.
,点E在弧AD上,射线AE与CD的延长线交于点F.
(1)求圆O的半径;
(2)如果AE=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )
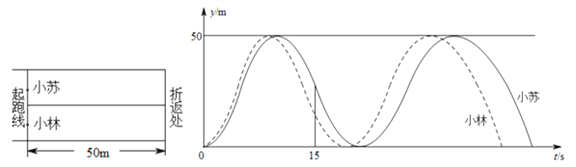
A. 两人从起跑线同时出发,同时到达终点.
B. 小苏跑全程的平均速度大于小林跑全程的平均速度.
C. 小苏在跑最后100m的过程中,与小林相遇2次.
D. 小苏前15s跑过的路程小于小林前15s跑过的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF、DF
(1)求证:BF是⊙A的切线.
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:
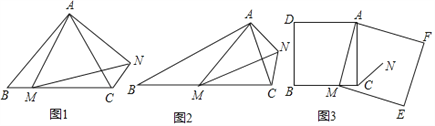
如图1,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为__________;
(2)深入探究:
如图2,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;
(3)拓展延伸:
如图3,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN=![]() ,试求EF的长.
,试求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,将一个直角的顶点置于点
,将一个直角的顶点置于点![]() ,并将它绕着点
,并将它绕着点![]() 旋转,两条直角边分别交射线
旋转,两条直角边分别交射线![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,联结
,联结![]() 交
交![]() 于点
于点![]() ,设
,设![]() .
.
(1)当![]() 时,求
时,求![]() 的长;
的长;
(2)若![]() ,求
,求![]() 关于
关于![]() 的函数关系式及定义域;
的函数关系式及定义域;
(3)旋转过程中,若![]() ,求此时
,求此时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点
,点![]() 是直线
是直线![]() 上的一个动点(点
上的一个动点(点![]() 与点
与点![]() 不重合),以
不重合),以![]() 为腰作等腰直角
为腰作等腰直角![]() ,连接
,连接![]() .
.
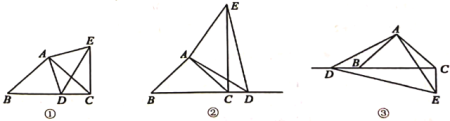
(1)如图①,当点![]() 在线段
在线段![]() 上时,直接写出
上时,直接写出![]() 的位置关系,线段
的位置关系,线段![]() ,
,![]() 之间的数量关系;
之间的数量关系;
(2)如图②,当点![]() 在线段
在线段![]() 的延长线上时,试判断线段
的延长线上时,试判断线段![]() ,
,![]() 的位置关系,线段
的位置关系,线段![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)如图③,当点![]() 在线段
在线段![]() 的延长线上时,试判断线段
的延长线上时,试判断线段![]() 的位置关系,线段
的位置关系,线段![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com