
【题目】(1)模型建立:
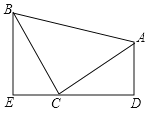
如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() .求证:
.求证:![]() ;
;
(2)模型应用:
①如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,以线段
,以线段![]() 为腰在第一象限内作等腰直角三角形
为腰在第一象限内作等腰直角三角形![]() ,则
,则![]() 点的坐标为___________(直接写出结果)
点的坐标为___________(直接写出结果)
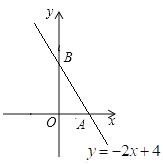
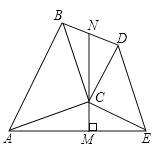
②如图,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 、
、![]() ,作
,作![]() 于
于![]() 点,延长
点,延长![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证:![]() 是
是![]() 的中点.
的中点.
【答案】(1)见解析;(2)①![]() 或
或![]() ,②见解析
,②见解析
【解析】
(1)利用同角的余角相等判断出∠CAD=∠BCE,然后利用AAS证明全等,即可得出结论;
(2)①先求出点A和点B的坐标,得到BO=4,AO=2,由![]() 为等腰直角三角形,可分为两种情况:AB=AC或AB=BC,分别求出点C坐标即可;
为等腰直角三角形,可分为两种情况:AB=AC或AB=BC,分别求出点C坐标即可;
②作![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]() 于
于![]() ,先由AAS证明
,先由AAS证明![]() ≌
≌![]() ,得到
,得到![]() ,同理可证
,同理可证![]() ,则
,则![]() ,然后证明
,然后证明![]() ≌
≌![]() ,即可得到结论.
,即可得到结论.
解:(1)![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
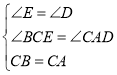 ,
,
![]() ;
;
(2)①∵一次函数![]() 的图象分别与
的图象分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,
,
令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ;
;
∴点A为(2,0),点B为(0,4),
∴BO=4,AO=2;
∵![]() 为等腰直角三角形,
为等腰直角三角形,
当AB=AC时,有∠BAC=90°,如图:
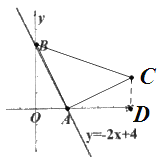
与(1)同理,得△ABO≌△CAD,
∴AD=BO=4,CD=AO=2,
∴OD=AO+AD=2+4=6,
∴点C的坐标为:![]() ;
;
当AB=BC时,有∠ABC=90°,如图:
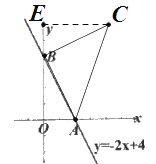
与(1)同理,得△ABO≌△BCE,
∴CE=BO=4,BE=AO=2,
∴OE=2+4=6,
∴点C坐标为:![]() ;
;
故答案为:![]() 或
或![]() .
.
②如图,作![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]() 于
于![]() ,
,
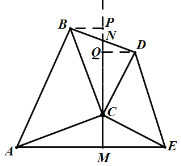
![]() ,
,
![]() ,
,
![]() ;
;
在![]() 与
与![]() 中,
中,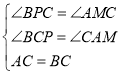 ,
,
![]() ,
,
![]() ,
,
同理,![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中,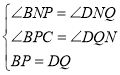 ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的中点.
的中点.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】已知y+2与x成正比例,且x=-2时,y=0
(1)求y与x之间的函数表达式,并画出函数的图象;
(2)利用图象直接写出:当y>0时,x的取值范围;
(3)设点P在y轴负半轴上,(2)中的图象与x轴,y轴分别交于A,B两点,且S△ABP=4,求P点的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在ABCD中,∠D=45°,E为BC上一点,连接AC,AE,
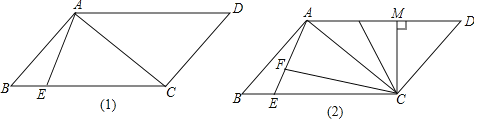
(1)若AB=2![]() ,AE=4,求BE的长;
,AE=4,求BE的长;
(2)如图2,过C作CM⊥AD于M,F为AE上一点,CA=CF,且∠ACF=∠BAE,求证:AF+AB=![]() AM.
AM.
查看答案和解析>>
科目:初中数学 来源: 题型:
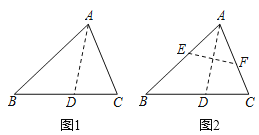
【题目】(1)观察与发现:
小明将三角形纸片![]() (
(![]() )沿过点
)沿过点![]() 的直线折叠,使得
的直线折叠,使得![]() 落在
落在![]() 边上,折痕为
边上,折痕为![]() ,展开纸片(如图1);在第一次的折叠基础上第二次折叠该三角形纸片,使点
,展开纸片(如图1);在第一次的折叠基础上第二次折叠该三角形纸片,使点![]() 和点
和点![]() 重合,折痕为
重合,折痕为![]() ,展平纸片后得到
,展平纸片后得到![]() (如图2).小明认为
(如图2).小明认为![]() 是等腰三角形,你同意他的结论吗?请说明理由:
是等腰三角形,你同意他的结论吗?请说明理由:
(2)模型与运用:
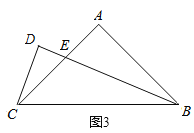
如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
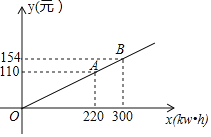
【题目】某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过220kWh时实行“基础电价”;第二档是当用电量超过220kWh时,其中的220kWh仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为xkWh时,应交电费为y元.具体收费情况如图所示,请根据图象回答下列问题:
(1)“基础电价”是 元/kwh;
(2)求出当x>220时,y与x的函数解析式;
(3)若小豪家六月份缴纳电费121元,求小豪家这个月用电量为多少kWh?
查看答案和解析>>
科目:初中数学 来源: 题型:
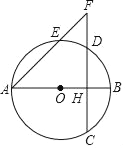
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足H在半径OB上,AH=5,CD=![]() ,点E在弧AD上,射线AE与CD的延长线交于点F.
,点E在弧AD上,射线AE与CD的延长线交于点F.
(1)求圆O的半径;
(2)如果AE=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:
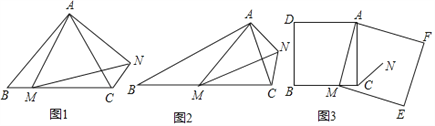
如图1,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为__________;
(2)深入探究:
如图2,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;
(3)拓展延伸:
如图3,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN=![]() ,试求EF的长.
,试求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com