
【题目】如图1,在ABCD中,∠D=45°,E为BC上一点,连接AC,AE,
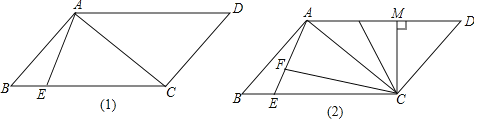
(1)若AB=2![]() ,AE=4,求BE的长;
,AE=4,求BE的长;
(2)如图2,过C作CM⊥AD于M,F为AE上一点,CA=CF,且∠ACF=∠BAE,求证:AF+AB=![]() AM.
AM.
【答案】(1)2![]() -2;(2)见解析
-2;(2)见解析
【解析】
(1)如图(1),过A作AH⊥BC于H,解直角三角形即可得到结论;
(2)如图(2),在AM上截取MN=MC,在△ACF内以AF为底边作等腰直角三角形AFP,连接CP,根据平行线的性质函数三角形的内角和得到∠CAN=∠PAC,求得∠APC=∠FPC=![]() =135°=∠ANC,根据全等三角形的性质得到AP=AN,于是得到结论.
=135°=∠ANC,根据全等三角形的性质得到AP=AN,于是得到结论.
解:(1)如图(1),过A作AH⊥BC于H,
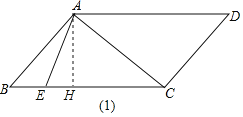
在ABCD中,∠D=∠B=45°,AB=2![]() ,
,
∴AH=BH=2![]() ,
,
∵AE=4,
∴EH=![]() =2,
=2,
∴BE=BH-EH=2![]() -2;
-2;
(2)如图(2),在AM上截取MN=MC,在△ACF内以AF为底边作等腰直角三角形AFP,连接CP,

∵∠AFC+∠FAC+∠ACF=180°,∠B+∠FAC+∠BAF+∠CAN=180°,
∴∠AFC=∠B+∠CAN=45°+∠CAN,
∵∠FAC=∠FAP+∠PAC=45°+∠PAC,∴∠FAC=∠∠AFC,
∴∠CAN=∠PAC,
∵∠APC=∠FPC=![]() =135°=∠ANC,
=135°=∠ANC,
∴△APC≌△ANC(AAS),
∴AP=AN,
∵AM=AN+MN,
∴![]() AM=
AM=![]() AN+
AN+![]() MN=AF+CD=AF+AB,
MN=AF+CD=AF+AB,
即AF+AB=![]() AM.
AM.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,若顶点B的纵坐标为2![]() ,∠B=60°,OC=
,∠B=60°,OC=![]() AC.
AC.
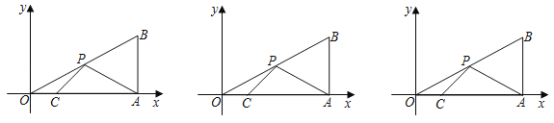
(1)请写出A、B、C三点的坐标;
(2)点P是斜边OB上的一个动点,则△PAC的周长的最小值为多少?
(3)若点P是OB的中点,点E在AO边上,将△OPE沿PE翻折,使得点O落在O'处,当O'E⊥AC时,在坐标平面内是否存在一点Q,使得△BAQ≌△O′PE,若存在,请直接写出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 与直线
与直线![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,
,![]() 与
与![]() 互补.
互补.
(1)试判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)如图2,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() ,求证:
,求证:![]() .
.
(3)如图3,在(2)的条件下,连接![]() ,
,![]() 是
是![]() 上一点使
上一点使![]() ,作
,作![]() 平分
平分![]() ,求
,求![]() 的度数.
的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:

(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店出售一种水果,经过市场估算,若每个售价为20元时,每周可卖出300个.经过市场调查,如果每个水果每降价1元,每周可多卖出25个,若设每个水果的售价为x元(x<20).
(1)则这一周可卖出这种水果为________个(用含x的代数式表示);
(2)若该周销售这种水果的收入为6400元,那么每个水果的售价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)模型建立:
如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() .求证:
.求证:![]() ;
;
(2)模型应用:
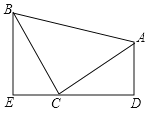
①如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,以线段
,以线段![]() 为腰在第一象限内作等腰直角三角形
为腰在第一象限内作等腰直角三角形![]() ,则
,则![]() 点的坐标为___________(直接写出结果)
点的坐标为___________(直接写出结果)
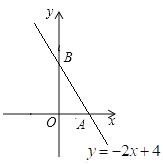
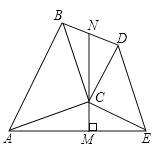
②如图,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 、
、![]() ,作
,作![]() 于
于![]() 点,延长
点,延长![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证:![]() 是
是![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
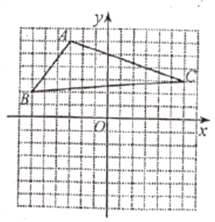
【题目】如图,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
. ![]() 与
与![]() 关于
关于![]() 轴对称,
轴对称,![]() 与
与![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 、
、![]() 、
、![]() 分别是点
分别是点![]() 、
、![]() 、
、![]() 的对应点,点
的对应点,点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的对应点.
的对应点.
(1)画出![]() 与
与![]() ,并写出点
,并写出点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,求六边形
,求六边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com