
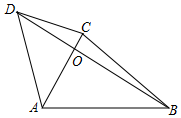
 如图,点O是四边形ABCD对角线AC、BD的交点,∠BAD与∠ACB互补,$\frac{OD}{OB}$=$\frac{3}{5}$,AD=6,AB=7,AC=5,则BC的长为$\frac{50}{7}$.
如图,点O是四边形ABCD对角线AC、BD的交点,∠BAD与∠ACB互补,$\frac{OD}{OB}$=$\frac{3}{5}$,AD=6,AB=7,AC=5,则BC的长为$\frac{50}{7}$. 分析 过点O作OM∥AD交AB于M根据平行线分线段成比例定理得到AM=$\frac{3}{8}$×7=$\frac{21}{8}$,BM=$\frac{5}{8}$×7=$\frac{35}{8}$,根据相似三角形的性质得到OM=$\frac{15}{4}$,再根据相似三角形的性质得到$\frac{BC}{OM}=\frac{AC}{AM}$,于是得到结论.
解答 解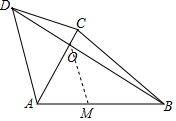 :过点O作OM∥AD交AB于M
:过点O作OM∥AD交AB于M
∴$\frac{BM}{AM}=\frac{OB}{OD}$=$\frac{5}{3}$,
∴AM=$\frac{3}{8}$×7=$\frac{21}{8}$,BM=$\frac{5}{8}$×7=$\frac{35}{8}$,
∵△BOM∽△BDA,
∴$\frac{BO}{BD}=\frac{OM}{AD}$,
∴OM=$\frac{15}{4}$,
∵∠BADO+∠MA=180°,∠BAD+∠ACB=180°,
∴∠OMA=∠ACB,
∴△AMO∽△ACB,
∴$\frac{BC}{OM}=\frac{AC}{AM}$,
∴BC=$\frac{50}{7}$.
故答案为:$\frac{50}{7}$.
点评 本题考查了相似三角形的判定和性质,熟练正确相似三角形的判定和性质是解题的关键.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个滑雪者从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,测得的一些数据(如表)
一个滑雪者从山坡滑下,为了得出滑行距离s(单位:m)与滑行时间t(单位:s)之间的关系式,测得的一些数据(如表)| 滑行时间t/s | 0 | 1 | 2 | 3 | 4 |
| 滑行距离s/m | 0 | 4.5 | 14 | 28.5 | 48 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
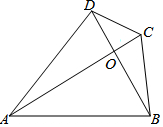 如图,在Rt△ABO中,∠AOB=90°,AO+BO=5,延长AO到C,使OC=3,延长BO到D,使OD=4,连接BC、CD、DA,则四边形ABCD面积的最大值为18.
如图,在Rt△ABO中,∠AOB=90°,AO+BO=5,延长AO到C,使OC=3,延长BO到D,使OD=4,连接BC、CD、DA,则四边形ABCD面积的最大值为18.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
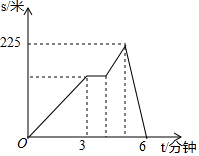 小明和小龙沿着一条笔直的马路进行长跑比赛,小明在比赛过程中始终领先小龙,并匀速跑完了全程,小龙匀速跑了几分钟后提速和小明保持速度一致,又过了1分钟,小龙因为体力问题,不得已又减速,并一直以这一速度完成了余下的比赛,完成比赛所用时间比小明多了1分钟,已知小明起跑后4分20秒时领先小龙175米,小明与小龙之间的距离s(单位:米)与他们所用时间t(单位:分钟)之间的函数关系如图所示.
小明和小龙沿着一条笔直的马路进行长跑比赛,小明在比赛过程中始终领先小龙,并匀速跑完了全程,小龙匀速跑了几分钟后提速和小明保持速度一致,又过了1分钟,小龙因为体力问题,不得已又减速,并一直以这一速度完成了余下的比赛,完成比赛所用时间比小明多了1分钟,已知小明起跑后4分20秒时领先小龙175米,小明与小龙之间的距离s(单位:米)与他们所用时间t(单位:分钟)之间的函数关系如图所示.| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果$\overrightarrow{AB}$=$\overrightarrow{CD}$,那么|$\overrightarrow{AB}$|=|$\overrightarrow{CD}$| | B. | $\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{b}$+$\overrightarrow{a}$ | ||
| C. | 如果非零向量$\overrightarrow{a}$=k•$\overrightarrow{b}$(k≠0),那么$\overrightarrow{a}$∥$\overrightarrow{b}$ | D. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com