
【题目】如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.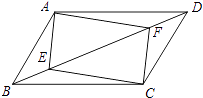
(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;
(2)若四边形AECF是菱形,则四边形ABCD是菱形吗?请说明理由?
(3)若四边形AECF是矩形,则四边形ABCD是矩形吗?不必写出理由.
【答案】
(1)
证明:连接AC交BD于点O,如图所示:
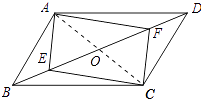
∵四边形AECF是平行四边形,
∴OA=OC,OE=OF,
∵BE=DF,
∴OB=OD,
∴四边形ABCD是平行四边形
(2)
解:理由如下:
∵四边形AECF是菱形,
∴AC⊥BD,
由(1)知,四边形ABCD是平行四边形;
∴四边形ABCD是菱形
(3)
解:四边形ABCD不是矩形;理由如下:
∵四边形AECF是矩形,
∴OA=OC,OE=OF,AC=EF,
∴OA=OC=OE=OF,
∵BE=DF,
∴OB=OD,
∴AC<BD,
∴四边形ABCD是平行四边形,不是矩形
【解析】(1)连接AC交BD于点O,由平行四边形的性质得出OA=OC,OE=OF,再证出OB=OD,即可得出结论;(2)由菱形的性质得出AC⊥BD,即可得出结论;(3)由矩形的性质得出OA=OC=OE=OF,证出OB=OD,AC<BD,得出四边形ABCD是平行四边形,不是矩形.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】用10根等长的火柴棒拼成一个三角形(火柴棒不允许剩余,重叠和折断),这个三角形一定是( )
A.等边三角形B.等腰三角形C.直角三角形D.不等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 和直线
和直线![]() 都经过A(1,0),B(﹣2,3)两点.
都经过A(1,0),B(﹣2,3)两点.
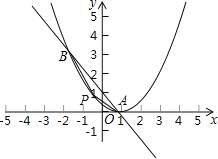
(1)求抛物线y1及直线y2的解析式;
(2)点P是抛物线上一动点,在直线AB的下方,当△PAB的面积最大时,请求出P点坐标;
(3)抛物线上是否存在一点M,使△MAB与△OAB的面积相等?若存在,请求出M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金堂县毗河城区河道整治工程长度为6.3km,起于毗河三桥,止于毗河与中河汇口处,机械清淤量为64万方,人工清淤量为0.5万方,沿线土方开挖3.5万方;该工程于2018年12月5日开工,预计竣工日期为2019年4月30日,则64万用科学记数法表示为( )
A.0.64×106B.6.4×106C.64×103D.6.4×105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com