
【题目】如图,已知抛物线![]() 和直线
和直线![]() 都经过A(1,0),B(﹣2,3)两点.
都经过A(1,0),B(﹣2,3)两点.
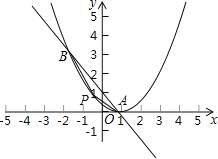
(1)求抛物线y1及直线y2的解析式;
(2)点P是抛物线上一动点,在直线AB的下方,当△PAB的面积最大时,请求出P点坐标;
(3)抛物线上是否存在一点M,使△MAB与△OAB的面积相等?若存在,请求出M点的坐标;若不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
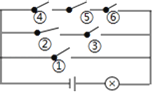
【题目】如图,电路图上有编号为①②③④⑤⑥共6个开关和一个小灯泡,闭合开关①或同 时闭合开关②③或同时闭合开关④⑤⑥都可使小灯泡发光,则任意闭合电路上其中的两个开关,小灯泡发光的概率为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
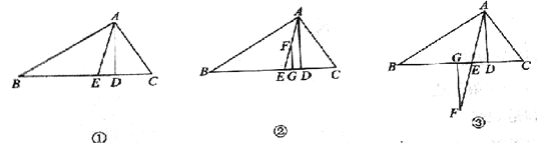
【题目】已知:△ABC中,AE平分∠BAC。
(1)如图①AD⊥BC于D,若∠C =70°,∠B =30°,求∠DAE的度数
(2)如图②所示,在△ABC中AD⊥BC,AE平分∠BAC,F是AE上的任意一点,过F作FG⊥BC于G,且∠B=40°,∠C=80°,求∠EFG的度数;
(3)在(2)的条件下,若F点在AE的延长线上(如图③),其他条件不变,则∠EFG的角度大小发生改变吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
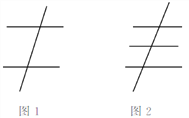
【题目】探究题:
(1)如图1,两条水平的直线被一条竖直的直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对;
(2)如图2,三条水平的直线被一条竖直的直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对;
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.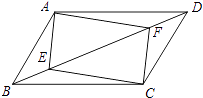
(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;
(2)若四边形AECF是菱形,则四边形ABCD是菱形吗?请说明理由?
(3)若四边形AECF是矩形,则四边形ABCD是矩形吗?不必写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
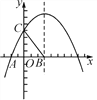
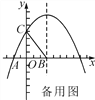
【题目】(本题满分10分)如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴的一个交点为A(-2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B.
(1)求抛物线的函数表达式;
(2)经过B,C的直线l平移后与抛物线交于点M,与x轴交于点N,当以B,C,M,N为顶点的四边形是平行四边形时,求出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com