
【题目】如图,将矩形ABCD绕点A顺时针旋转到矩形AB'C'D'的位置,旋转角为![]() (0°<
(0°<![]() <90°).若∠1=112°,则∠
<90°).若∠1=112°,则∠![]() 的大小是( )
的大小是( )
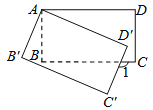
A. 22° B. 20° C. 28° D. 68°
科目:初中数学 来源: 题型:
【题目】两块等腰直角三角形纸片AOB和COD按图①所示放置,直角顶点重合在点O处,AB=25.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图②所示.
(1)在图②中,求证:AC=BD,且AC⊥BD;
(2)当BD与CD在同一直线上(如图③)时,若AC=7,求CD的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,﹣2),B(﹣2,﹣4),C(﹣4,﹣1).
(1)把△ABC向上平移2个单位长度,再向右平移1个单位长度后得到△A1B1C1,请画出△A1B1C1,并写出点A1,B1,C1的坐标;
(2)求△A1B1C1的面积;
(3)点P在坐标轴上,且△A1B1P的面积是2,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,直线
,直线![]() 和直线
和直线![]() 交于点C、D,直线
交于点C、D,直线![]() 上有一点P.
上有一点P.
(1)如图1,点P在C、D之间运动时,∠PAC、∠APB、∠PBD之间有什么关系?并说明理由。
(2)若点P在C、D两点外侧运动时(P点与C、D不重合,如图2、3),试直接写出∠PAC、∠APB、∠PBD之间有什么关系,不必写理由。

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,直线![]() ,
,![]() ,
,![]() 分别通过A,B,C三点,且
分别通过A,B,C三点,且![]() ,若
,若![]() 与
与![]() 的距离为5,
的距离为5,![]() 与
与![]() 的距离为7,则正方形ABCD的面积等于( )
的距离为7,则正方形ABCD的面积等于( )

A. 148 B. 70 C. 144 D. 74
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1计算:![]() ;
;
(2)解不等式组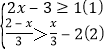
请结合题意填空,完成本题的解答:
解不等式(1),得______________.
解不等式(2),得_______________.
把不等式(1)和(2)的解集在数轴上表示出来
![]()
∴原不等式组的解集为_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校门前正对一条公路,车流量较大,为便于学生安全通过,特建一座人行天桥.如图,是这座天桥的引桥部分示意图,上桥通道由两段互相平行的楼梯AB、CD和一段平行于地面的平台CB构成.已知∠A=37°,天桥高度DH为5.1米,引桥水平跨度AH为8.3米.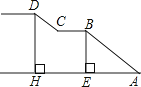
(1)求水平平台BC的长度;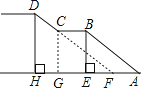
(2)若两段楼梯AB:CD=10:7,求楼梯AB的水平宽度AE的长.
(参考数据:sin37°≈ ![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com