
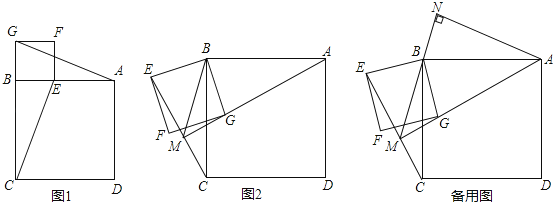
【题目】(1)如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,求证:![]() =
=![]() .
.
(2)如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若![]() ,则
,则![]() 的值为 .
的值为 .
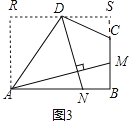
(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=12,BC=CD=4,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,易证AP=EF,GH=BQ,△PDA∽△QAB,然后运用相似三角形的性质就可解决问题;
(2)只需运用(1)中的结论,就可得到![]() ,就可解决问题;
,就可解决问题;
(3)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,易证四边形ABSR是矩形,由(1)中的结论可得![]() .设SC=x,DS=y,则AR=BS=4+x,RD=12-y,在Rt△CSD中根据勾股定理可得x2+y2=16①,在Rt△ARD中根据勾股定理可得(4+x)2+(12-y)2=144②,解①②就可求出x,即可得到AR,问题得以解决.
.设SC=x,DS=y,则AR=BS=4+x,RD=12-y,在Rt△CSD中根据勾股定理可得x2+y2=16①,在Rt△ARD中根据勾股定理可得(4+x)2+(12-y)2=144②,解①②就可求出x,即可得到AR,问题得以解决.
解:(1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,
∵四边形ABCD是矩形,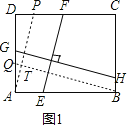
∴AB∥DC,AD∥BC.
∴四边形AEFP、四边形BHGQ都是平行四边形,
∴AP=EF,GH=BQ.
又∵GH⊥EF,
∴AP⊥BQ,
∴∠QAT+∠AQT=90°.
∵四边形ABCD是矩形,
∴∠DAB=∠D=90°,
∴∠DAP+∠DPA=90°,
∴∠AQT=∠DPA.
∴△PDA∽△QAB,
∴![]() ,
,
∴![]() =
=![]() .
.
(2)如图2,
∵EF⊥GH,AM⊥BN,
∴由(1)中的结论可得![]() =
=![]() ,
,![]() =
=![]() ;
;
∴![]() ,
,
故答案为![]() ;
;
(3)过点D作平行于AB
则四边形ABSR是平行四边形.
∵∠ABC=90°,
∴平行四边形ABSR是矩形,
∴∠R=∠S=90°,RS=AB=12,AR=BS.
∵AM⊥DN,
∴由(1)中的结论可得 ![]() .
.
设SC=x,DS=y,则AR=BS=4+x,RD=12﹣y,
∴在Rt△CSD中,x2+y2=16①,
在Rt△ARD中,(4+x)2+(12﹣y)2=144②,
由②﹣①得x=3y﹣4③,
解方程组 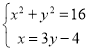 ,得
,得![]() (舍去),或
(舍去),或 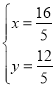 ,
,
∴AR=4+x=![]()
∴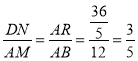 .
.


科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
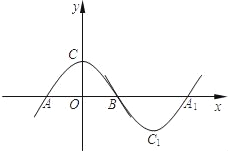
A. ab=﹣2 B. ab=﹣3 C. ab=﹣4 D. ab=﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
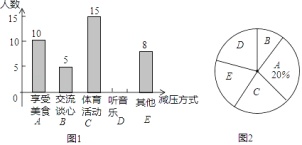
![]() 九年级接受调查的同学共有多少名,并补全条形统计图;
九年级接受调查的同学共有多少名,并补全条形统计图;
![]() 九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
![]() 若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
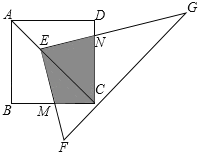
【题目】如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD边长为1.则重叠部分四边形EMCN的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、BEFG均为正方形.
(1)如图1,连接AG、CE,试判断AG和CE的数量关系和位置关系为 (直接写结果)
(2)将正方形BEFG绕点B顺时针旋转β角(0°<β<180°),如图2,连接AG、CE相交于点M,连接MB,当角β发生变化时,AG和CE的数量关系和位置关系是否发生变化?请说明理由.
(3)在(2)的条件下,如备用图,连接MB,过点A作AN⊥MB交MB的延长线于点N,若MB=3![]() ,正方形ABCD的边长为3
,正方形ABCD的边长为3![]() ,求BN的长.
,求BN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小飞研究二次函数y=-(x-m)2-m+1(m为常数)性质时如下结论:①这个函数图象的顶点始终在直线y=-x+1上;②存在一个m的值,使得函数图象的顶点与![]() 轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )
轴的两个交点构成等腰直角三角形;③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2>2m,则y1<y2;④当-1<x<2时,y随x的增大而增大,则m的取值范围为m≥2其中错误结论的序号是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽泰州”的工作部署,市政府计划对城区道路进行改造,现安排甲、乙两个工程队完成该改造工作.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造720米的道路比乙队改造同样长的道路少用4天.
倍,甲队改造720米的道路比乙队改造同样长的道路少用4天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,若需改造的道路全长2400米,改造总费用不超过195万元,则至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,点B在函数y=![]() (k>0,x>0)的图象上,点P(m,n)是函数y=
(k>0,x>0)的图象上,点P(m,n)是函数y=![]() (k>0,x>0)的图象上任一点,过点P分别作x轴、y轴的垂线,垂足分别为E,F,并设矩形OEPF和正方形OABC不重合部分的面积为S.
(k>0,x>0)的图象上任一点,过点P分别作x轴、y轴的垂线,垂足分别为E,F,并设矩形OEPF和正方形OABC不重合部分的面积为S.

(1)求点B的坐标和k的值;
(2)当S=![]() 时,求点P的坐标;
时,求点P的坐标;
(3)写出S关于m的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com