
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ’ΐΖΫ–ΈOABCΒΡΟφΜΐΈΣ9Θ§ΒψOΈΣΉχ±ξ‘≠ΒψΘ§ΒψA‘Ύx÷α…œΘ§ΒψC‘Ύy÷α…œΘ§ΒψB‘ΎΚ· ΐyΘΫ![]() (kΘΨ0Θ§xΘΨ0)ΒΡΆΦœσ…œΘ§ΒψP(mΘ§n) «Κ· ΐyΘΫ
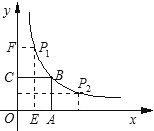
(kΘΨ0Θ§xΘΨ0)ΒΡΆΦœσ…œΘ§ΒψP(mΘ§n) «Κ· ΐyΘΫ![]() (kΘΨ0Θ§xΘΨ0)ΒΡΆΦœσ…œ»Έ“ΜΒψΘ§ΙΐΒψPΖ÷±πΉςx÷αΓΔy÷αΒΡ¥ΙœΏΘ§¥ΙΉψΖ÷±πΈΣEΘ§FΘ§≤Δ…ηΨΊ–ΈOEPFΚΆ’ΐΖΫ–ΈOABC≤Μ÷ΊΚœ≤ΩΖ÷ΒΡΟφΜΐΈΣS.
(kΘΨ0Θ§xΘΨ0)ΒΡΆΦœσ…œ»Έ“ΜΒψΘ§ΙΐΒψPΖ÷±πΉςx÷αΓΔy÷αΒΡ¥ΙœΏΘ§¥ΙΉψΖ÷±πΈΣEΘ§FΘ§≤Δ…ηΨΊ–ΈOEPFΚΆ’ΐΖΫ–ΈOABC≤Μ÷ΊΚœ≤ΩΖ÷ΒΡΟφΜΐΈΣS.

(1)«σΒψBΒΡΉχ±ξΚΆkΒΡ÷ΒΘΜ
(2)Β±SΘΫ![]() ±Θ§«σΒψPΒΡΉχ±ξΘΜ
±Θ§«σΒψPΒΡΉχ±ξΘΜ
(3)–¥≥ωSΙΊ”ΎmΒΡΚ· ΐ±μ¥ο ΫΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©Θ®3,3Θ©Θ§![]() Θ®2Θ©
Θ®2Θ©![]() Θ§
Θ§![]() Θ®3Θ©
Θ®3Θ©![]() Μρ
Μρ![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΖ¥±»άΐΚ· ΐ÷–’ΐΖΫ–ΈΒΡΟφΜΐ”κΖ¥±»άΐœΒ ΐΒΡΙΊœΒΘ§Φ¥Ω…«σΒΟΖ¥±»άΐΚ· ΐΫβΈω ΫΘ§ΫχΕχ«σΒΟBΒΡΉχ±ξΘΜ
Θ®2Θ©Ζ÷ΝΫ÷÷«ιΩωΖ÷±π«σΫβ.
Θ®3Θ©ΗυΨί(2)Φ¥Ω…–¥≥ωΚ· ΐΫβΈω ΫΘ°
ΫβΘΚ(1)ΓΏ’ΐΖΫ–ΈOABCΒΡΟφΜΐΈΣ9Θ§
ΓύOA=OC=3Θ§
ΓύB(3,3).
”÷ΓΏΒψB(3,3)‘ΎΚ· ΐ![]() (k>0,x>0)ΒΡΆΦœσ…œΘ§
(k>0,x>0)ΒΡΆΦœσ…œΘ§
Γύk=9.
(2)Ζ÷ΝΫ÷÷«ιΩωΘΚΔΌΒ±ΒψP1‘ΎΒψBΒΡΉσ≤ύ ±Θ§
ΓΏP1(m,n)‘ΎΚ· ΐ![]() …œΘ§
…œΘ§
Γύmn=9.
Γύ‘ρ![]()
Γύ![]()
Γύn=6.
Γύ![]()
ΔΎΒ±ΒψP2‘ΎΒψBΜρBΒΡ”“≤ύ ±Θ§
ΓΏP2(m,n)‘ΎΚ· ΐ![]() …œΘ§
…œΘ§
Γύmn=9.
Γύ![]()
Γύn=![]() Θ§
Θ§
Γύm=6.
Γύ![]()
(3)Β±0<m<3 ±Θ§![]() 93mΘΜ
93mΘΜ
Β±![]() ±Θ§
±Θ§ ![]()
ΓΏn=![]()
![]()
![]()
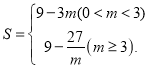



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®1Θ©»γΆΦ1Θ§ΨΊ–ΈABCD÷–Θ§EFΓΆGHΘ§EFΖ÷±πΫΜABΘ§CD”ΎΒψEΘ§FΘ§GHΖ÷±πΫΜADΘ§BC”ΎΒψGΘ§HΘ§«σ÷ΛΘΚ![]() ΘΫ
ΘΫ![]() Θ°
Θ°
Θ®2Θ©»γΆΦ2Θ§‘Ύ¬ζΉψΘ®1Θ©ΒΡΧθΦΰœ¬Θ§”÷AMΓΆBNΘ§ΒψMΘ§NΖ÷±π‘Ύ±ΏBCΘ§CD…œΘ§»τ![]() Θ§‘ρ
Θ§‘ρ![]() ΒΡ÷ΒΈΣΓΓ ΓΓΘ°
ΒΡ÷ΒΈΣΓΓ ΓΓΘ°
Θ®3Θ©»γΆΦ3Θ§ΥΡ±Ώ–ΈABCD÷–Θ§ΓœABCΘΫ90ΓψΘ§ABΘΫADΘΫ12Θ§BCΘΫCDΘΫ4Θ§AMΓΆDNΘ§ΒψMΘ§NΖ÷±π‘Ύ±ΏBCΘ§AB…œΘ§«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈOABC»ΤΉ≈ΒψOΡφ ±’κ–ΐΉΣ40ΓψΒΟΒΫ’ΐΖΫ–ΈODEFΘ§Ν§Ϋ”AFΘ§«σΓœOFAΒΡΕ» ΐ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕΰ¥ΈΚ· ΐ![]() ΒΡΆΦœσ»γΆΦΥυ ΨΘ§‘ρœ¬
ΒΡΆΦœσ»γΆΦΥυ ΨΘ§‘ρœ¬
Ν–Ϋα¬έΘΚΔΌ![]() Θ§ΔΎ
Θ§ΔΎ![]() Θ§Δέ
Θ§Δέ![]() Θ§Δή
Θ§Δή![]() Θ§Δί
Θ§Δί![]()
![]() ÷–’ΐ»ΖΒΡ «Θ® Θ©
÷–’ΐ»ΖΒΡ «Θ® Θ©

A. ΔΎΔήΔί B. ΔΌΔΎΔή C. ΔΌΔέΔή D. ΔΌΔέΔήΔί
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
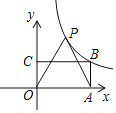
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–ΈOABCΒΡΕΞΒψA,CΖ÷±π‘Ύx÷αΘ§y÷α…œΘ§ΕΞΒψB‘ΎΒΎ“ΜœσœόΘ§AB=1.ΫΪœΏΕΈOA»ΤΒψOΑ¥Ρφ ±’κΖΫœρ–ΐΉΣ60ΓψΒΟΒΫœΏΕΈOP,Ν§Ϋ”AP,Ζ¥±»άΐΚ· ΐ![]() Θ®kΓΌ0Θ©ΒΡΆΦœσΨ≠ΙΐP,BΝΫΒψΘ§‘ρkΒΡ÷ΒΈΣ______________.
Θ®kΓΌ0Θ©ΒΡΆΦœσΨ≠ΙΐP,BΝΫΒψΘ§‘ρkΒΡ÷ΒΈΣ______________.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
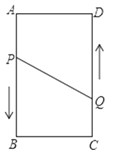
ΓΨΧβΡΩΓΩ»γΆΦΘ§AΓΔBΓΔCΓΔDΈΣΨΊ–ΈΒΡΥΡΗωΕΞΒψΘ§AB=16cmΘ§AD=6cmΘ§Ε·ΒψPΓΔQΖ÷±π¥”ΒψAΓΔCΆ§ ±≥ωΖΔΘ§ΒψP“‘3cm/sΒΡΥΌΕ»œρΒψB“ΤΕ·Θ§“Μ÷±ΒΫ¥οBΈΣ÷ΙΘ§ΒψQ“‘2 cm/sΒΡΥΌΕ»œρD“ΤΕ·Θ°
Θ®1Θ©PΓΔQΝΫΒψ¥”≥ωΖΔΩΣ ΦΒΫΦΗΟκΘΩΥΡ±Ώ–ΈPBCQΒΡΟφΜΐΈΣ33cm2ΘΜ
Θ®2Θ©PΓΔQΝΫΒψ¥”≥ωΖΔΩΣ ΦΒΫΦΗΟκ ±ΘΩΒψPΚΆΒψQΒΡΨύάκ «10cmΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈ“Ο«Ε®“εΘΚ”–“ΜΉιΕ‘Ϋ«œύΒ»ΕχΝμ“ΜΉιΕ‘Ϋ«≤ΜœύΒ»ΒΡΆΙΥΡ±Ώ–ΈΫ–ΉωΓΑΒ»Ε‘Ϋ«ΥΡ±Ώ–ΈΓ±Θ°
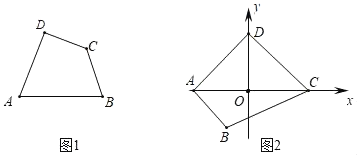
Θ®1Θ©“―÷ΣΘΚ»γΆΦ1Θ§ΥΡ±Ώ–ΈABCD «ΓΑΒ»Ε‘Ϋ«ΥΡ±Ώ–ΈΓ±Θ§ΓœAΓΌΓœCΘ§ΓœAΘΫ75ΓψΘ§ΓœDΘΫ85ΓψΘ§‘ρΓœCΘΫΓΓ ΓΓΘ°
Θ®2Θ©“―÷ΣΘΚ‘ΎΓΑΒ»Ε‘Ϋ«ΥΡ±Ώ–ΈΓ±ABCD÷–Θ§ΓœDABΘΫ60ΓψΘ§ΓœABCΘΫ90ΓψΘ§ABΘΫ4Θ§ADΘΫ3Θ°«σΕ‘Ϋ«œΏACΒΡ≥ΛΘ°
Θ®3Θ©“―÷ΣΘΚ»γΆΦ2Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§ΥΡ±Ώ–ΈABCD «ΓΑΒ»Ε‘Ϋ«ΥΡ±Ώ–ΈΓ±Θ§Τδ÷–AΘ®©¹2Θ§0Θ©ΓΔCΘ®2Θ§0Θ©ΓΔBΘ®©¹1Θ§©¹![]() Θ©Θ§ΒψD‘Ύy÷α…œΘ§≈ΉΈοœΏyΘΫax2+bx+cΘ®aΘΦ0Θ©ΙΐΒψAΓΔDΘ§«“Β±©¹2ΓήxΓή2 ±Θ§Κ· ΐyΘΫax2+bx+c»ΓΉν¥σ÷ΒΈΣ3Θ§«σΕΰ¥ΈœνœΒ ΐaΒΡ÷ΒΘ°
Θ©Θ§ΒψD‘Ύy÷α…œΘ§≈ΉΈοœΏyΘΫax2+bx+cΘ®aΘΦ0Θ©ΙΐΒψAΓΔDΘ§«“Β±©¹2ΓήxΓή2 ±Θ§Κ· ΐyΘΫax2+bx+c»ΓΉν¥σ÷ΒΈΣ3Θ§«σΕΰ¥ΈœνœΒ ΐaΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§ΒψAΒΡΉχ±ξΈΣΘ®0Θ§7Θ©Θ§ΒψBΒΡΉχ±ξΈΣΘ®0Θ§3Θ©Θ§ΒψCΒΡΉχ±ξΈΣΘ®3Θ§0Θ©Θ°

Θ®1Θ©‘ΎΆΦ÷–Ής≥ωΓςABCΒΡΆβΫ”‘≤Θ®±ΘΝτ±Ί“ΣΒΡΉςΆΦΚέΦΘΘ§≤Μ–¥ΉςΖ®Θ©Θ§‘≤–ΡΉχ±ξΈΣ ______ΘΜ
Θ®2Θ©»τ‘Ύx÷αΒΡ’ΐΑκ÷α…œ”–“ΜΒψDΘ§«“ΓœADB=ΓœACBΘ§‘ρΒψDΒΡΉχ±ξΈΣ ______Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§Ε‘”ΎΒψPΘ®xΘ§yΘ©Θ§»γΙϊΒψQΘ®xΘ§yΓδΘ©ΒΡΉίΉχ±ξ¬ζΉψyΓδΘΫ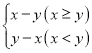 Θ§Ρ«Ο¥≥ΤΒψQΈΣΒψPΒΡΓΑΙΊΝΣΒψΓ±Θ°
Θ§Ρ«Ο¥≥ΤΒψQΈΣΒψPΒΡΓΑΙΊΝΣΒψΓ±Θ°
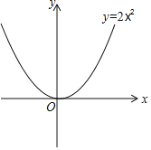
Θ®1Θ©«κ÷±Ϋ”–¥≥ωΒψΘ®3Θ§5Θ©ΒΡΓΑΙΊΝΣΒψΓ±ΒΡΉχ±ξΓΓ ΓΓΘΜ
Θ®2Θ©»γΙϊΒψP‘ΎΚ· ΐyΘΫx©¹2ΒΡΆΦœσ…œΘ§ΤδΓΑΙΊΝΣΒψΓ±Q”κΒψP÷ΊΚœΘ§«σΒψPΒΡΉχ±ξΘΜ
Θ®3Θ©»γΙϊΒψMΘ®mΘ§nΘ©ΒΡΓΑΙΊΝΣΒψΓ±N‘ΎΚ· ΐyΘΫ2x2ΒΡΆΦœσ…œΘ§Β±0ΓήmΓή2 ±Θ§«σœΏΕΈMNΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com